이번에는 삼각형 안의 점 개수를 빠르게 세는 테크닉(Counting Points in Triangle)에 대해서 다룬다. 이 테크닉에 붙은 이름은 아직까지는 없는 것으로 알고 있다. 따라서 이 글의 제목도 공식적으로 굳어진 명칭이 아니다.
다음과 같은 문제를 생각해 보자.
$2$차원 좌표평면에 속한 점 $n$개가 주어진다. 어떤 세 점도 일직선상에 있지 않다. 이제 여기서 세 개의 점을 골라서 삼각형을 만들면 그 삼각형은 다른 점들을 포함할 수도 있다. 이때 점을 $0, 1, \ldots, n - 3$개 포함하는 삼각형의 개수를 모두 구하여라.
점 $n$개로 만들 수 있는 서로 다른 삼각형의 수는 $\frac{n(n - 1)(n - 2)}{6} = \frac{1}{6}n^3 - \frac{1}{2}n^2 + \frac{1}{3}n$이고, 삼각형마다 $n$개의 점 각각을 포함하는지 일일이 확인한다면 시간복잡도는 $\Theta(n^4)$가 나오게 된다. 하지만 이런 문제들의 제한은 보통 $\Theta(n^4)$ 풀이를 막도록 설계되기 때문에 웬만하면 써먹기 어려울 것이다.
여기서는 $\Theta(n^3)$ 시간에 이 문제를 해결하는 방법을 살펴볼 것이다. 먼저 한 개의 점을 고정하고, 그 점을 꼭짓점으로 가지는 모든 삼각형에 대해 삼각형이 포함하는 점의 개수를 구했다고 하자. 여기까지는 $\Theta(n^3)$ 시간에 할 수 있다. (참고로 점이 삼각형 안에 포함되는지 확인하는 연산은 세 변과 점을 기준으로 CCW 부호가 모두 동일한지 확인하는 방법을 쓰면 다소 무겁긴 하지만 상수 시간에 가능하다.)
여기서 계산한 값들을 잘 더하고 빼면 나머지 모든 삼각형이 포함하는 점의 개수를 전부 알 수 있다는 것이 이 테크닉의 중요한 부분이다. 아래 그림을 보자.

점 $\text{A}$가 고정되어 있고, $\text{A}$를 꼭짓점으로 가지는 삼각형들이 포함하는 점의 개수를 각각 구한 상태라고 한다면 삼각형 $\color{#FF0000}{\text{ABC}}$가 포함하는 점의 개수 $\color{#FF0000}a$, 삼각형 $\color{#00C000}{\text{ABD}}$가 포함하는 점의 개수 $\color{#00C000}b$, 삼각형 $\color{#0000FF}{\text{ACD}}$가 포함하는 점의 개수 $\color{#0000FF}c$는 알고 있다. 여기서 삼각형 $\text{BCD}$가 포함하는 점의 개수 $d$는 $\color{#00C000}b + \color{#0000FF}c - \color{#FF0000}a$와 같다.

이런 경우는 식이 약간 달라진다. 계산해 보면 $d = \color{#0000FF}c - \color{#FF0000}a - \color{#00C000}b - 1$임을 알 수 있다. 마지막에 $1$을 빼는 이유는 $c$에 점 $\text{B}$가 포함되어 있기 때문이다.
이 두 가지 경우를 변형하면 모든 삼각형에 대해서 답을 구할 수 있는데 회전이 많아지면 그만큼 처리해야 하는 경우도 늘어나므로 최대한 적은 경우만 생기도록 하는 것이 좋다. 예를 들어 점들을 좌표 순서대로 정렬하고 첫 번째 점을 $\text{A}$로 고정하고 나머지 점들이 정렬된 순서를 유지한다고 하면 앞서 살펴본 경우 외에 다음과 같은 경우들만 추가된다. 이래도 $5$가지 경우를 처리해야 하지만 이중 두 가지는 식이 같아서 한번에 처리할 수 있는데다 $\text{A}$가 가운데에도 들어갈 수 있는 상황을 처리하는 것보다는 나을 것이다.
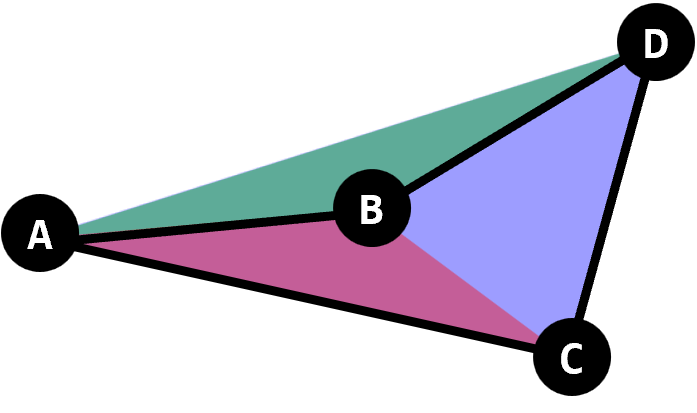
이 경우는 바로 앞의 경우와 같은 식으로 $d$를 구할 수 있다.

이런 경우도 생길 수 있고 이때 $d = \color{#FF0000}a + \color{#0000FF}c - \color{#00C000}b$이다.

마지막으로 이런 경우가 생길 수 있고 이때 $d = \color{#00C000}b - \color{#FF0000}a - \color{#0000FF}c - 1$이다. 이 경우도 아까와 같은 이유로 $b$에 점 $\text{C}$가 포함되어 있어서 마지막에 $1$을 빼 준다.
각각의 경우에 $d$는 상수 시간에 구할 수 있고 삼각형의 개수가 $O(n^3)$이므로 이걸 모든 삼각형에 대해서 반복해도 $O(n^3)$ 시간에 답을 다 구할 수 있게 된다.
구현은 다음과 같다. 중간중간에 있는 주석을 잘 참고하자.
#import<bits/stdc++.h>
using namespace std;
typedef long long LL;
struct Point{LL x, y;} p[504];
int a[504][504];
int C(Point a, Point b){return a.x < b.x || a.x == b.x && a.y < b.y;}
int ccw(Point p1, Point p2, Point p3)
{
LL t = (p2.x - p1.x) * (p3.y - p1.y) - (p3.x - p1.x) * (p2.y - p1.y);
if(t > 0)return 1;
else if(t < 0)return -1;
else return 0; // 세 점이 한 직선에 있지 않으므로 실제로 이 줄에는 도달하지 않아야 함
}
int f(int x, int y, int z)
{
if(x > y)swap(x, y);
if(y > z)swap(y, z);
if(x > y)swap(x, y); // x < y < z인 상태를 유지. 같은 값이 두 개 이상 들어오는 경우는 없다고 가정함
if(x == 1)return a[y][z];
int c021 = ccw(p[1], p[y], p[x]);
int c231 = ccw(p[y], p[z], p[x]);
int c301 = ccw(p[z], p[1], p[x]);
int c032 = ccw(p[1], p[z], p[y]);
if(c021 == c231 && c231 == c301)return a[y][z] - a[x][y] - a[x][z] - 1; // Case 2, 3
else if(c021 == c231 && c231 == c032)return a[x][z] - a[x][y] - a[y][z] - 1; // Case 5
else if(c021 == c032)return a[x][y] + a[y][z] - a[x][z]; // Case 4
else return a[x][z] + a[y][z] - a[x][y]; // Case 1
}
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)cin >> p[i].x >> p[i].y;
sort(p + 1, p + n + 1, C);
for(int i = 2; i <= n; i++)
{
for(int j = i + 1; j <= n; j++) // p[1], p[i], p[j]로 이루어지는 삼각형이 포함하는 점의 개수 a[i][j] 계산
{
for(int k = 2; k <= n; k++) // p[1]은 확인할 필요가 없다.
{
int x = ccw(p[1], p[i], p[k]) + ccw(p[i], p[j], p[k]) + ccw(p[j], p[1], p[k]);
if(x == 3 || x == -3)a[i][j]++; // ccw 함수의 결과가 모두 CW가 나오거나 모두 CCW가 나온 경우에만 점이 삼각형 안에 있음
}
}
}
}
[참고 링크]
[연습문제]
BOJ 14164. 삼각형 영역 (Platinum I) [샘플 코드]
가장 기본적인 문제이다. 점을 $0, 1, \ldots, n - 3$개 포함하는 삼각형의 개수를 모두 구하면 된다.
BOJ 23249. Triangles (Platinum I)
이번에는 점을 하나 이상 포함하는 삼각형의 개수만 세면 된다. 그래서 스위핑으로도 풀 수 있다고 하는데, 스위핑 풀이는 아직 잘 모른다.
BOJ 26104. Empty Quadrilaterals (Diamond IV)
이번에는 점을 포함하지 않는 사각형의 개수를 세야 한다. 사각형은 삼각형 두 개로 분할할 수 있기 때문에 두 점을 잇는 변 $\frac{n(n - 1)}{2}$개에 대해서 한쪽에 있는 삼각형들과 그 반대쪽에 있는 삼각형들 중 다른 점을 포함하지 않는 삼각형의 개수를 각각 세서 곱한 다음 다 더하면 되는데 이렇게 하면 오목사각형은 한 번만 세는 반면 볼록사각형은 두 번 세기 때문에 점을 포함하지 않는 볼록사각형과 오목사각형이 몇 개인지도 구해야 한다. 그러려면 변을 기준으로 양쪽에 있는 삼각형을 확인할 때 점들을 각도에 따라 정렬하고 투 포인터로 처리하면 되는데 구현량이 상당히 많아지고 정교한 처리도 필요하게 되므로 주의해야 한다.
'Algorithm > J. Optimization' 카테고리의 다른 글
| 195. Small to Large Technique (0) | 2024.07.11 |
|---|---|
| 194. Optimization Intro (2) | 2024.07.08 |

