볼록 껍질을 이용해서 $2$차원 좌표에서 가장 먼 두 점을 찾는 방법을 알아보자. 점이 $n$개인 경우 $\frac{n(n-1)}{2}$개의 쌍을 전부 다 확인하는 방법이 있지만, 점의 개수가 $10$만 개 정도를 넘어가면 속도가 너무 느리다. 이럴 때 사용할 수 있는 방법으로 회전하는 캘리퍼스(Rotating Calipers)라는 알고리즘이 잘 알려져 있다. 캘리퍼스는 길이를 잴 때 사용하는 컴퍼스와 비슷하게 생긴 도구이고, 회전하는 캘리퍼스라고 하면 이런 도구를 회전시키면서 길이를 잰다는 의미로 해석할 수 있다. 실제 알고리즘의 동작 과정도 이와 비슷하며 다음과 같다.
1. 점들의 볼록 껍질을 찾고, 여기에 속하는 점들을 꼭짓점으로 하는 볼록 다각형이 있다고 가정한다. 볼록 껍질에 $k$개의 점이 속해 있다고 하자.
2. 볼록 다각형의 각 변에 시계 방향으로 $1$번부터 $k$번까지 번호를 매긴다. $1$번 변은 아무거나 선택해도 상관 없다. 또한 볼록 껍질을 이루는 $k$개의 점에도 번호를 매긴다. $i$번 변이 $i$번 점과 $(i \,\bmod\, k) + 1$번 점을 연결한다고 하자. 번호를 매겼다면 임의의 서로 다른 두 변을 선택한다. 선택한 변의 번호가 각각 $x$, $y$라고 하자. 이제 두 개의 캘리퍼스가 $x$번과 $y$번 변에 있는 것으로 간주하고 캘리퍼스를 회전하면서 점들 사이의 최장 거리를 구할 것이다.
3. $x$번 점, $(x \,\bmod\, k) + 1$번 점, $y$번 점, $(y \,\bmod\, k) + 1$번 점을 각각 $\text{A}$, $\text{B}$, $\text{C}$, $\text{D}$라고 하면, $x$번 변은 점 $\text{A}$와 점 $\text{B}$를 지나고 $y$번 변은 점 $\text{C}$와 점 $\text{D}$를 지난다. 점 $\text{A}$와 점 $\text{C}$ 사이의 거리를 잰 다음, $x$번 변과 $y$번 변이 평행이 아닌 경우 두 변을 길게 연장해 교점 $\text{E}$를 찾는다.
4. $x$번 변과 $y$번 변이 평행한 경우 아무 캘리퍼스나 하나를 다음 변으로 옮긴다. 여기서 $i$번 변의 다음 변은 $(i \,\bmod\, k) + 1$번 변을 의미한다. 만약 $x$번 변과 $y$번 변이 평행하지 않고 교점 $\text{E}$가 존재한다면, $\text{E}$가 $\text{B}$와 $\text{C}$보다 $\text{A}$와 $\text{D}$에 더 가까이 있을 경우 $x$번 변에 있는 캘리퍼스를 다음 변으로 옮기고, 그렇지 않다면 $y$번 변에 있는 캘리퍼스를 다음 변으로 옮긴다.
5. 3번과 4번 과정을 반복하다가 어떤 점들 사이의 거리를 두 번째로 쟀다면 실행을 종료한다. 잰 거리가 가장 길게 나오는 두 점이 이 좌표평면에서 가장 먼 두 점이 된다.
글이 뭔가 복잡하게 적혀 있다. 증명이 필요한 부분들도 존재한다. 예시를 통해서 조금 더 자세하게 알아보자.
첫 번째로 확인해야 할 부분은 2번 과정에 깔린 '좌표평면에서 가장 먼 두 점은 둘 다 볼록 껍질에 속한다'는 전제이다. 직관적으로 와닿을 수도 있지만 증명이 그렇게 복잡하지 않으므로 한번 짚고 넘어가기로 한다.
- 좌표평면에서 가장 먼 두 점이 $\text{A}$와 $\text{B}$이고 $\text{B}$가 볼록 껍질에 속하지 않는다고 가정하자. $\text{A}$에서 $\text{B}$ 쪽으로 반직선을 그으면 볼록 껍질과 $\text{A}$를 제외한 한 점에서 만나게 된다. 이 점을 $\text{C}$라고 하면 $\text{B}$가 볼록 껍질에 속하지 않으므로 $|\overline{\text{AB}}| < |\overline{\text{AC}}|$이다.
- 만약 $\text{C}$가 볼록 껍질에 속하는 점과 겹치면 $\text{A}$와 $\text{B}$ 사이의 거리보다 $\text{A}$와 $\text{C}$ 사이의 거리가 더 멀기 때문에 $\text{A}$와 $\text{B}$는 가장 먼 두 점이 될 수 없다. 만약 $\text{C}$가 볼록 껍질에 속하지 않는다면 $\text{C}$는 볼록 껍질의 어떤 변 위의 한 점이다. 이 변의 양 끝점 중 $\angle \text{C} \ge 90^\circ$가 되게 하는 점을 $\text{D}$라고 하자.
- $\angle \text{C} \ge 90^\circ$이므로 $\angle \text{C}$의 대변인 $\overline{\text{AD}}$가 삼각형 $\text{ACD}$의 세 변 중 가장 긴 변이다. 따라서 $|\overline{\text{AD}}| > |\overline{\text{AC}}|$이므로 $|\overline{\text{AD}}| > |\overline{\text{AB}}|$이다. $\text{A}$와 $\text{D}$ 사이의 거리가 $\text{A}$와 $\text{B}$ 사이의 거리보다 길기 때문에 $\text{A}$와 $\text{B}$는 가장 먼 두 점이 될 수 없다.
- 볼록 껍질에 속하지 않는 어떤 점을 선택해도 같은 결과가 나오므로 가장 먼 두 점은 둘 다 볼록 껍질에 속해 있다.
두 번째로 알고리즘의 실행이 언젠가는 끝난다는 것을 보여야 한다. 이것은 쉽다. 두 변에 캘리퍼스를 놓을 수 있는 경우의 수는 $k^2$이므로 캘리퍼스를 $k^2$번 이상 움직인다면 비둘기집의 원리에 의해 이전에 두 캘리퍼스를 놓았던 변과 똑같은 두 변에 다시 캘리퍼스가 놓이는 상황이 발생한다. 또한 어떤 상황에서 캘리퍼스를 움직일 수 있는 경우의 수는 최대 $2$이다. 즉 캘리퍼스를 움직이는 과정은 상태 공간 사이의 이동으로 해석할 수 있고, 상태의 수가 $2k^2$ 이하이므로 상태 공간을 $2k^2$번 이상 이동한다면 두 번 이상 도달하는 상태가 반드시 존재한다. 이때 알고리즘의 실행을 종료하므로 이 알고리즘은 언젠가는 종료된다.
여기서 잠시 3번과 4번 과정을 분석하기로 한다. 먼저 임의의 두 변을 선택하고 캘리퍼스를 위치시킨다. $2$번과 $4$번 변에 캘리퍼스가 있다고 하자.

$2$번 점과 $4$번 점 사이의 거리를 잰다. $2$번과 $4$번 변은 평행하지 않으므로 캘리퍼스를 길게 늘려 교점을 찾는다. 교점이 $3$번과 $4$번 점 쪽에 있으므로 빨간색 캘리퍼스를 다음 변으로 옮긴다.

$2$번과 $5$번 점 사이의 거리를 잰다. $2$번과 $5$번 변은 평행하지 않으므로 캘리퍼스를 길게 늘려 교점을 찾는다. 다만 이 변들은 평행에 가까워서 교점이 너무 멀리 있기 때문에 그림에 교점이 나오지는 않았는데, 구해 보면 $2$번과 $6$번 점 쪽에 있다. 따라서 파란색 캘리퍼스를 다음 변으로 옮긴다.

$3$번과 $5$번 점 사이의 거리를 잰다. $4$번과 $6$번 변은 평행하지 않으므로 캘리퍼스를 길게 늘려 교점을 찾는다. 교점이 $4$번과 $5$번 점 쪽에 있으므로 빨간색 캘리퍼스를 다음 변으로 옮긴다.

같은 방법으로 길이를 재고 교점의 위치에 따라 둘 중 한 캘리퍼스를 다음 변으로 옮기는 과정을 반복한다.

돌리고

돌리고

돌리고

또 돌린다.

이때 자세히 보면 위에 두 캘리퍼스의 위치만 서로 바뀌어 있었던 상황이 있었다. 따라서 $2$번 점과 $5$번 점 사이의 거리는 두 번째로 재는 것이 되고, 여기서 캘리퍼스를 계속 돌려 봤자 이미 쟀던 점들 사이의 거리를 또 재기만 하고 점들 사이의 거리의 최댓값이 갱신되는 일은 더이상 없을 것이므로 알고리즘의 실행을 종료한다. 지금까지 잰 거리들(초록색 선) 중 가장 긴 것을 구하면 가장 먼 두 점을 찾을 수 있다.
다시 증명으로 돌아간다. 세 번째로 증명할 것은 3번과 4번 과정에서 거리를 잰 점 쌍들 중에 가장 먼 두 점이 있다는 사실인데, 일단 다음과 같은 관찰을 할 수 있다.
- 알고리즘의 실행이 종료되었을 때 두 번 거리를 잰 점을 각각 $\text{P}_1$, $\text{P}_2$라고 하자. 그렇다면 알고리즘의 실행 중 캘리퍼스가 각각 $\text{P}_1$번 변과 $\text{P}_2$번 변에 있었던 순간이 존재하고, 마지막에는 두 캘리퍼스가 위치를 바꿔서 각각 $\text{P}_2$번 변과 $\text{P}_1$번 변에 있었다는 것을 알 수 있다.
- 캘리퍼스는 알고리즘이 실행되는 동안 다음 변으로만 이동하므로 한 캘리퍼스는 $\text{P}_1, \text{P}_1 + 1, \ldots, \text{P}_2 - 1, \text{P}_2$번 변을 모두 지나고, 이때 $\text{P}_1, \text{P}_1 + 1, \ldots, \text{P}_2 - 1, \text{P}_2$번 점과 다른 점 사이의 거리를 한 번씩은 재게 된다. 마찬가지로 다른 캘리퍼스는 $\text{P}_2, \text{P}_2 + 1, \ldots, \text{P}_1 - 1, \text{P}_1$번 변을 모두 지나고, 이때 $\text{P}_2, \text{P}_2 + 1, \ldots, \text{P}_1 - 1, \text{P}_1$번 점과 다른 점 사이의 거리를 한 번씩은 재게 된다. 즉 알고리즘이 실행되는 동안 캘리퍼스가 한 번도 지나가지 않는 변은 없고, 다른 점과 거리를 한 번도 재지 않는 점도 없다.
- 알고리즘의 실행이 종료되었다면, 실행을 종료한 시점에서 캘리퍼스를 조건에 맞게 한 번 이상 움직였을 때 두 점 사이의 거리는 전부 앞에서 한 번 이상 잰 상태이다.
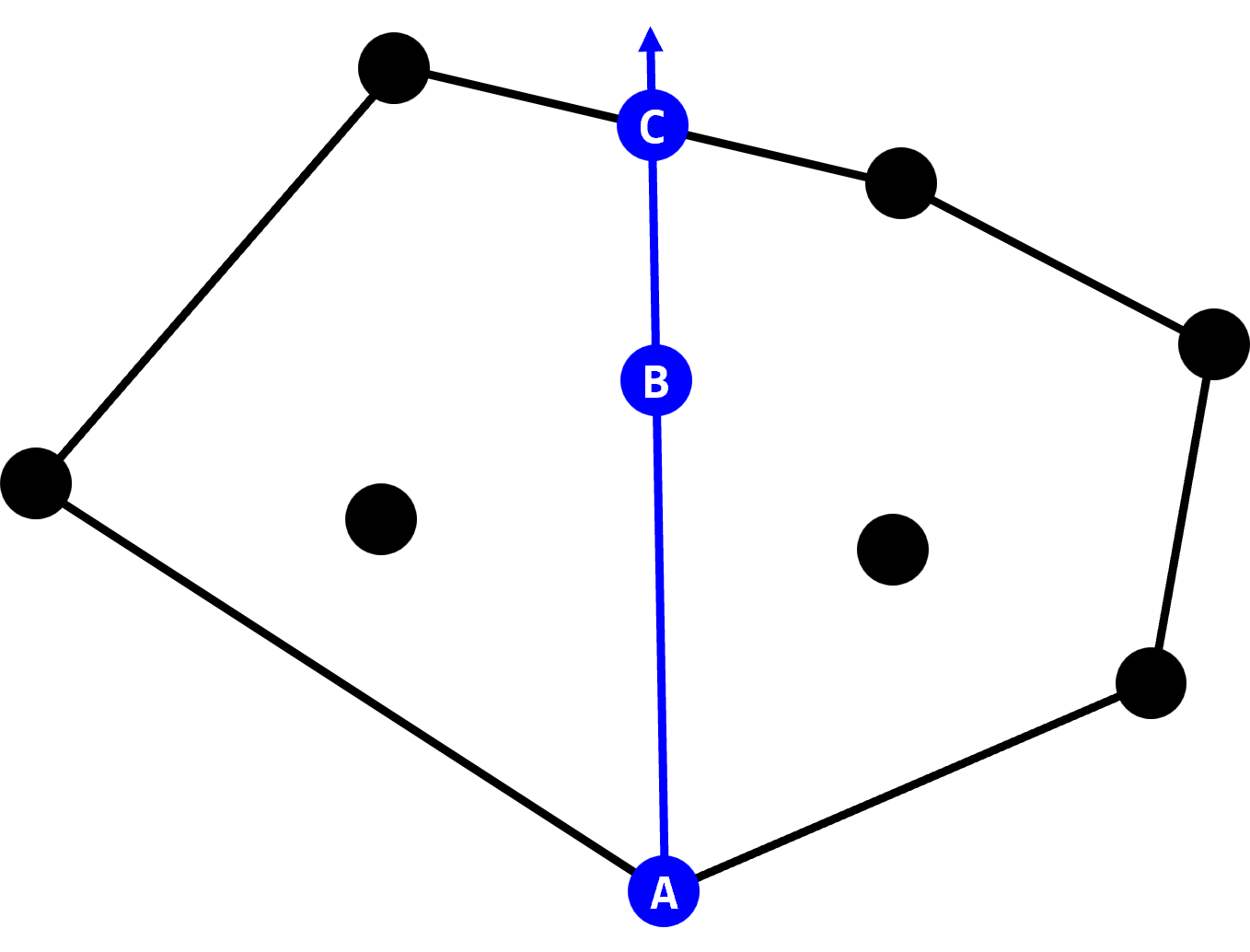
이제 한 점 $\text{B}$와 $\text{B}$에서 가장 먼 점 $\text{E}$가 존재하고, $\text{B}$의 이전 점과 다음 점이 각각 $\text{A}$와 $\text{C}$이고 $\text{E}$의 이전 점과 다음 점이 각각 $\text{D}$와 $\text{F}$라고 하자. 회색 선은 $\text{B}$를 지나면서 $\text{E}$에 평행한 직선과 $\text{E}$를 지나면서 $\text{B}$에 평행한 직선이다. 즉 두 회색 선은 서로 평행하다.

이제 두 캘리퍼스의 초기 위치를 다섯 가지 상태로 구분할 수 있다. 그림을 $180^\circ$ 회전했을 때 위상적으로 동일한 상태들은 같은 상태인 것으로 간주한다.
A. 두 캘리퍼스의 시작점(거리를 재는 점)이 $\text{B}$와 $\text{E}$인 경우
B. 한 캘리퍼스의 시작점이 $\text{B}$이고 다른 캘리퍼스의 시작점이 $\text{F} \sim \text{A}$ 사이에 있는 경우
C. 한 캘리퍼스의 시작점이 $\text{B}$이고 다른 캘리퍼스의 시작점이 $\text{C} \sim \text{D}$ 사이에 있는 경우
D. 두 캘리퍼스의 시작점이 $\text{F} \sim \text{A}$ 사이에 있는 경우
E. 한 캘리퍼스의 시작점이 $\text{F} \sim \text{A}$ 사이에 있고 다른 캘리퍼스의 시작점이 $\text{C} \sim \text{D}$ 사이에 있는 경우
우리의 목표는 모든 상태에서 $\text{B}$와 $\text{E}$ 사이의 거리를 한 번 이상 잰다는 사실을 보이는 것이다. 이것을 보일 수 있다면 볼록 껍질에 속한 각 점마다 그 점에서 가장 먼 점까지의 거리를 한 번 이상 재므로 그 중 거리가 최대가 되는 점이 가장 먼 두 점이 되고 알고리즘이 가장 먼 두 점을 잘 찾는다는 것을 확인할 수 있다. 그런데 이 상태들을 분석해 보면 서로 연결되어 있어서 모든 상태를 확인하는 게 생각보다 쉽다.
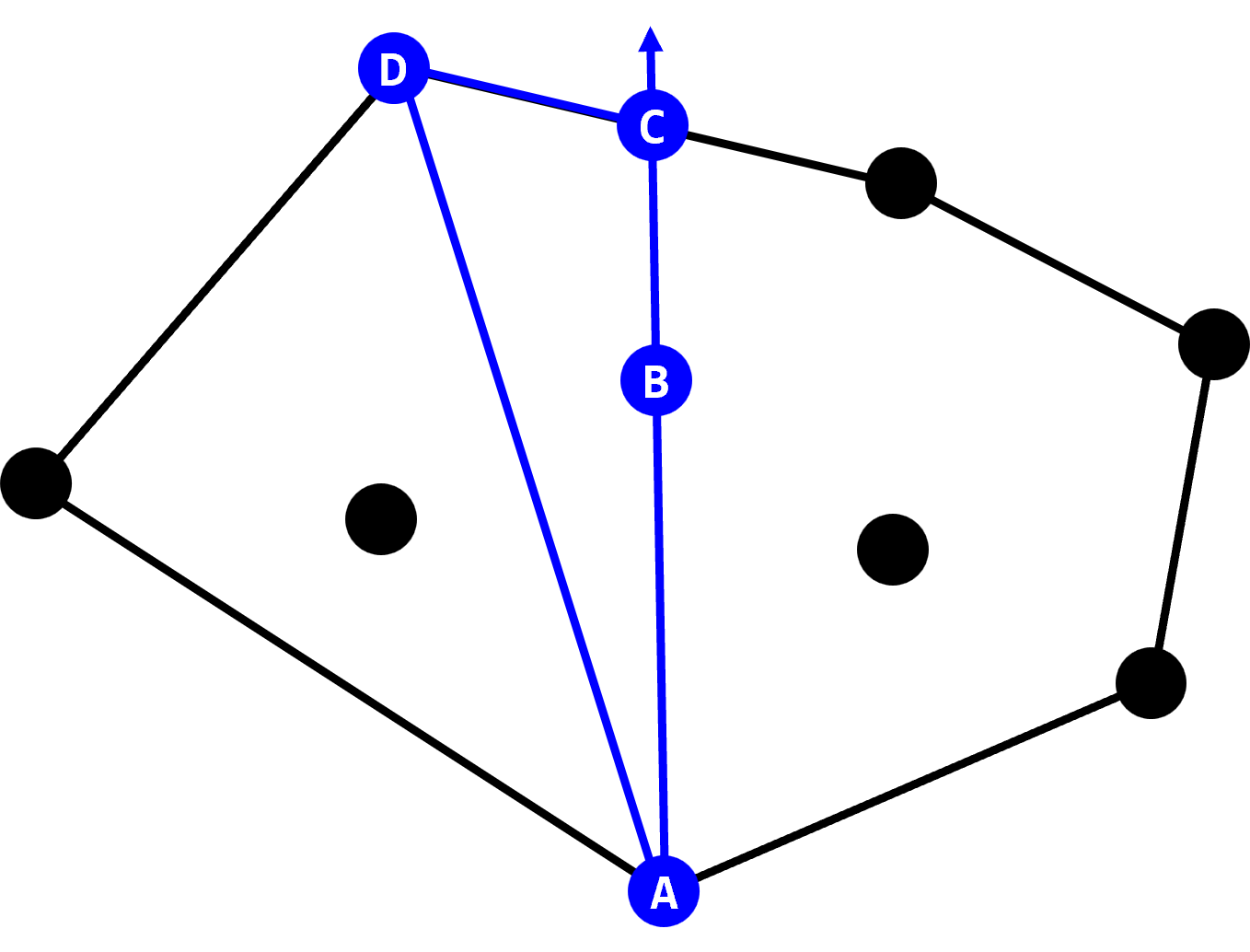
- 먼저 D의 경우 점 $\text{A}$ 쪽에 있는 캘리퍼스가 계속 움직이다가 선분 $\text{BC}$ 위에 위치하게 된다. 이 상태는 B와 같다.
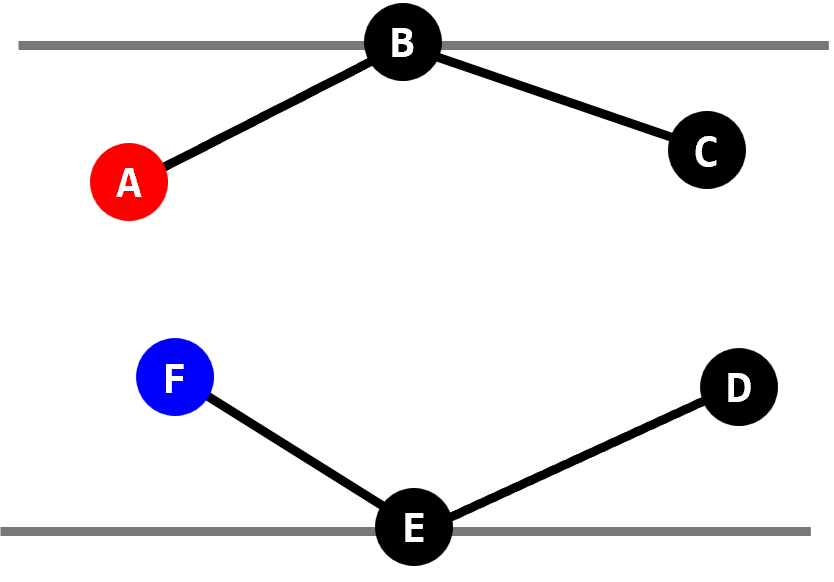
- 상태 B에서 시작점이 점 $\text{B}$에 있는 캘리퍼스가 한 번 움직이면 상태 E로 넘어간다.
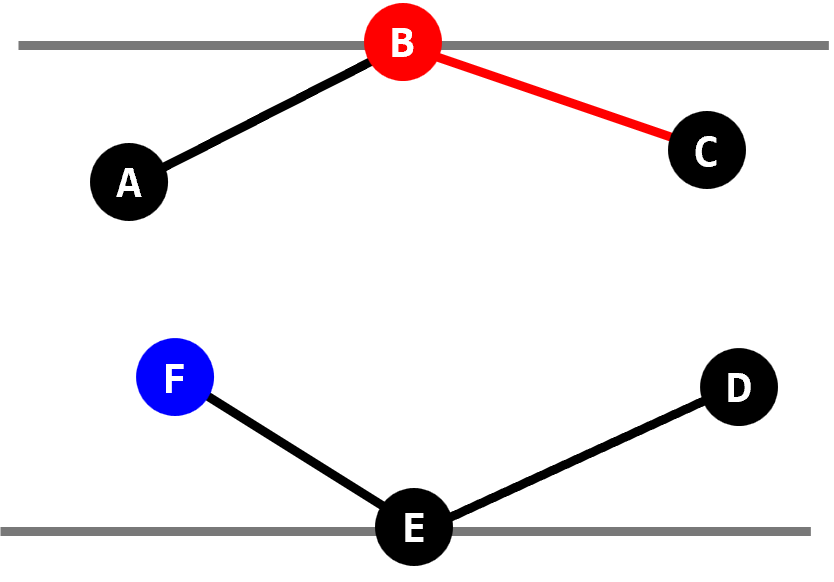
- 상태 E에서는 두 캘리퍼스 모두 움직일 수 있다. 한 가지 확실한 것은 캘리퍼스를 계속 움직이다 보면 시작점이 점 $\text{C}$와 $\text{D}$ 사이에 있는 캘리퍼스의 끝점이 점 $\text{E}$까지 움직이거나 시작점이 점 $\text{F}$와 점 $\text{A}$ 사이에 있는 캘리퍼스의 끝점이 점 $\text{B}$까지 움직이는 상황이 발생한다는 것이다. 그러면 그 상태는 C와 같다.
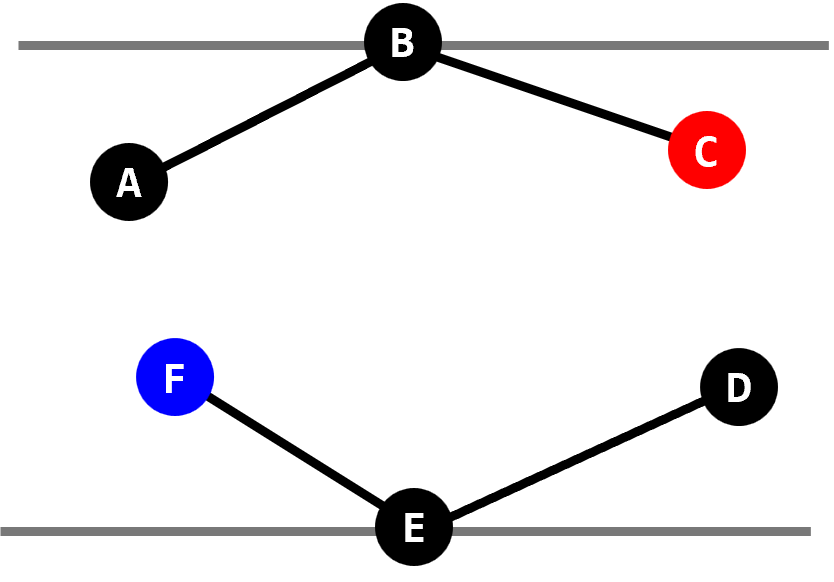
- 상태 C에서는 끝점이 점 $\text{C}$와 $\text{D}$ 사이에 있는 캘리퍼스가 계속 움직이다가 끝점이 $\text{E}$가 되면 상태 A로 바뀐다.
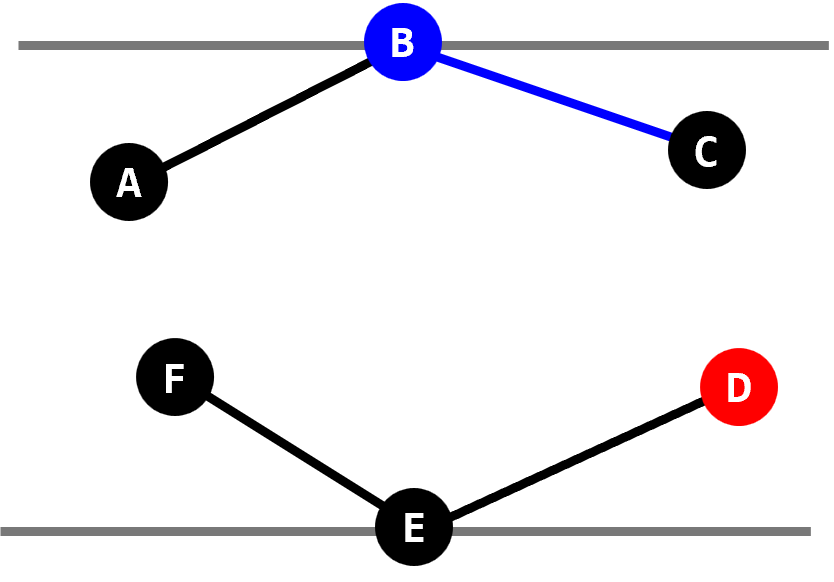
- 상태 A가 되었을 때 점 $\text{B}$와 $\text{E}$ 사이의 거리를 잰다.
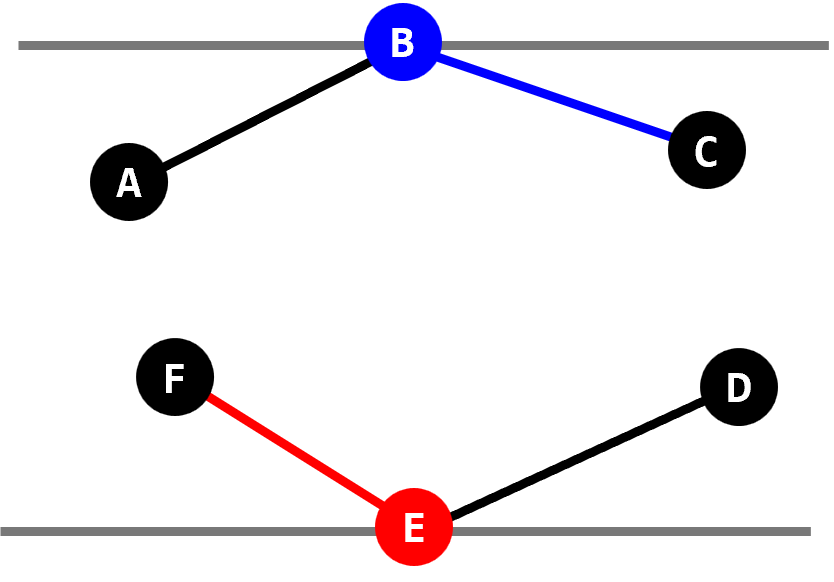
- 즉 상태들 사이에 $\text{D} \to \text{B} \to \text{E} \to \text{C} \to \text{A}$라는 관계가 성립하여 모든 상태에서 상태 $\text{A}$에 도달하고 상태 $\text{A}$에서 점 $\text{B}$와 $\text{E}$ 사이의 거리를 재므로 모든 상태에서 점 $\text{B}$와 $\text{E}$ 사이의 거리를 잰다는 사실이 확인되었다.
네 번째로 이 알고리즘이 충분히 빠르게 작동한다는 것을 증명해야 한다. 이를 위해 시간복잡도를 계산해 보자. 점 $n$개의 볼록 껍질을 구하는 것은 $\Theta(n \lg n)$ 시간에 할 수 있고, 캘리퍼스를 한 번 움직이는 것은 CCW 함수 등으로 $O(1)$ 시간에 할 수 있다. 따라서 알고리즘이 종료될 때까지 캘리퍼스가 몇 번 정도 움직이는지 구하면 시간복잡도를 알아낼 수 있다.
- 세 번째 증명에서 모든 상태가 상태 A로 이어짐을 보였다. 여기서 캘리퍼스가 계속 움직일 경우 상태 B, E, C를 거쳐서 다시 상태 A로 돌아온다. 이때 두 캘리퍼스는 위치만 서로 바뀌고 점 $\text{B}$와 점 $\text{E}$ 사이의 거리를 재는데, 이 거리는 이미 앞에서 한 번 이상 쟀을 것이므로 알고리즘이 아무리 오래 작동해도 여기서는 무조건 종료된다는 것을 알 수 있다. 이때 처음 상태 A가 된 다음 두 번째로 상태 A가 될 때까지 캘리퍼스가 움직인 횟수는 $k$회이다.
- 모든 상태들 중 상태 A로 이어지기까지 가장 오래 걸리는 상태는 D이고, 상태 D에서 상태 A까지 진행되는 동안 두 캘리퍼스 모두 한 바퀴 이상 움직이지 않으므로 임의의 상태에서 상태 A까지 진행되는 동안 캘리퍼스가 움직인 횟수는 $2k$ 이하이다.
- 임의의 상태에서 상태 A가 되었다가 다시 상태 A가 되면 알고리즘이 종료되며, 이 과정에서 캘리퍼스가 움직인 횟수는 $3k$ 이하이다. 물론 다시 상태 A가 되기 전에 알고리즘이 종료될 수도 있으며 캘리퍼스가 움직인 횟수가 $3k$ 이하인 것은 그대로이다.
즉 캘리퍼스를 움직이는 과정은 $O(k)$ 시간에 끝난다. $k \le n$이므로 볼록 껍질을 구한 상태에서 가장 먼 두 점을 구하는 과정의 시간복잡도는 $O(n)$이다. 따라서 $n$개의 점에서 가장 먼 두 점의 거리를 구하는 과정의 시간복잡도는 볼록 껍질을 구하는 과정과 동일한 $\Theta(n \lg n)$이다.
이제 점의 개수가 많아져도 가장 먼 두 점을 빠르게 구할 수 있다. 다만 현재 채점이 가능한 문제들 중 대다수는 작은 제한 또는 약한 데이터로 인해 $k$가 크지 않아서 볼록 껍질을 구한 다음 그냥 $\frac{k(k-1)}{2}$개의 두 점 쌍의 거리를 다 확인해 보는 방법으로도 풀린다고 한다.
구현은 다음과 같다. $n$개의 점들의 좌표를 입력받고 볼록 껍질을 구해서 벡터 $\text{v}$를 얻었다고 하자.
// 주의: 현재 이 코드는 컴파일해서 검증하지 않았기 때문에 틀린 부분이 존재할 수 있다.
int ccw(Point a, Point b, Point c, Point d)
{
LL t = (b.x - a.x) * (d.y - c.y) - (d.x - c.x) * (b.y - a.y);
if(t > 0)return 1;
else if(t < 0)return -1;
else return 0;
}
LL dist(Point a, Point b) // 두 점 사이의 거리의 제곱을 반환
{
return (b.x - a.x) * (b.x - a.x) + (b.y - a.y) * (b.y - a.y);
}
pair<int, int> getDiameter(const vector<int> &v)
{
int c1 = 0, c2 = 1, x = 0, y = 1, z = 0; // c1, c2: 캘리퍼스 / x, y: 현재까지 구한 가장 먼 두 점 / z: 플래그
LL m = dist(p[v[0]], p[v[1]]);
for(;;)
{
int w = ccw(p[v[c1]], p[v[(c1 + 1) % k]], p[v[c2]], p[v[(c2 + 1) % k]]);
if(w > 0)
{
c1++;
if(c1 == k)
{
c1 = 0;
z = 1;
}
}
else
{
c2++;
if(c2 == k)c2 = 0;
}
LL d = dist(p[v[c1]], p[v[c2]]);
if(d > m)
{
m = d;
x = c1;
y = c2;
}
if(z)break;
}
return {p[v[x]].i, p[v[y]].i};
}
[참고 링크]
[연습문제]
BOJ 2049. 가장 먼 두 점 (Platinum III)
회전하는 캘리퍼스로 가장 먼 두 점의 길이를 찾는다.
점의 개수가 늘어나고 좌표의 범위가 커졌다. 하지만 여전히 회전하는 캘리퍼스로 잘 통과한다.
BOJ 16525. Escape, Polygon! (Platinum II)
서로 다른 $3$개의 변을 선택하는 경우의 수 $_N\text{C}_3$에서 세 변의 연장선이 다각형을 완전히 감싸지 못하는 경우의 수를 회전하는 캘리퍼스로 세서 빼 주면 된다. 조금 섬세한 처리가 필요하고 구현 방식에 따라 오버플로우에 주의해야 할 수도 있다.
꽤 유명한 문제인데 아직 안 풀었다. 업데이트 예정
'Algorithm > G. Geometry' 카테고리의 다른 글
| 104. Voronoi Diagram & Delaunay Triangulation (0) | 2021.09.04 |
|---|---|
| 99. Andrew's Algorithm (2) | 2021.08.31 |
| 98. Graham Scan (0) | 2021.08.31 |
| 97. Convex Hull (0) | 2021.08.31 |
| 96. Line Intersection (4) | 2021.08.30 |



