106. Preorder Traversal

트리의 순회(Tree Traversal)는 루트 있는 트리에 존재하는 각각의 노드를 일정한 규칙에 따라 한 번씩 방문하는 과정을 의미한다. 일반적으로 트리의 순회는 모든 노드가 최대 두 개의 자식 노드를 갖는 이진 트리(Binary Tree) 구조에서 다루어지지만, 이진 트리가 아닌 트리에서도 순회를 할 수 있다. 순회는 루트 노드에서 시작하며 자식 노드에는 순서가 있다고 가정한다. 노드를 방문하는 규칙은 크게 세 가지가 있으며 규칙에 따라 트리 순회의 이름도 달라진다.

---

트리의 전위 순회(Preorder Traversal)^[각주:1]는 노드를 먼저 방문하고 각각의 자식 노드를 루트로 하는 서브트리를 차례로 방문하는 순회 방법이다.

 

다음과 같은 트리가 있을 때 전위 순회는 다음과 같은 순서로 진행된다.

루트 노드 $\text{D}$에서 순회를 시작한다. 먼저 노드 $\text{D}$를 방문하고, 첫 번째 자식 노드 $\text{G}$로 이동한다.

노드 $\text{G}$를 방문하고 자식 노드 $\text{I}$로 이동한다.

노드 $\text{I}$를 방문한다. 노드 $\text{I}$는 자식 노드가 없으므로 부모 노드로 되돌아간 다음 $\text{G}$의 다음 자식 노드 $\text{B}$로 이동한다.

노드 $\text{B}$를 방문하고 자식 노드 $\text{F}$로 이동한다.

노드 $\text{F}$를 방문한다. 노드 $\text{F}$는 자식 노드가 없으므로 부모 노드 $\text{B}$로 되돌아가는데, 노드 $\text{B}$의 남은 자식 노드가 없으므로 다시 부모 노드 $\text{G}$로 되돌아간다. 노드 $\text{G}$도 남은 자식 노드가 없으므로 부모 노드 $\text{D}$로 되돌아가서 다음 자식 노드 $\text{A}$로 이동한다.

같은 방법으로 나머지 노드들을 방문한다. (노드 $\text{A}$)

(노드 $\text{E}$)

(노드 $\text{J}$)

(노드 $\text{C}$)

(노드 $\text{H}$)

더이상 방문할 노드가 없으므로 탐색을 종료한다.

 

구현은 다음과 같다.

#import<bits/stdc++.h>
using namespace std;
vector<int>v, e[100005];
void preorder_traversal(int prev, int node)
{
    v.push_back(node);
    for(auto &p: e[node])
    {
        if(p != prev)preorder_traversal(p);
    }
}
int main()
{
    int n, root, x, y;
    cin >> n >> root;
    for(int i = 0; i < n - 1; i++)
    {
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }
    preorder_traversal(0, root);
}

어떤 문제들에서는 각각의 노드의 부모 노드가 주어지는데, 이 경우는 구현이 조금 더 간단하다. 대략 다음과 같은 형태이다.

#import<bits/stdc++.h>
using namespace std;
vector<int>v, e[100005];
void preorder_traversal(int node)
{
    v.push_back(node);
    for(auto &p: e[node])preorder_traversal(p);
}
int main()
{
    int n, x;
    cin >> n;
    for(int i = 2; i <= n; i++)
    {
        cin >> x;
        e[x].push_back(i);
    }
    preorder_traversal(1);
}

$1$번 노드가 루트이고 나머지 노드의 부모 노드가 차례로 입력되는 경우의 예시이다.

---

트리 순회의 개념은 식을 표현할 때 사용되기도 한다. 이때 식은 연산자에 대한 피연산자의 개수가 고정된 형태이다. 알기 쉽게 피연산자 $2$개를 갖는 산술 연산자($+, -, \times, \div$)로 이루어진 다음과 같은 식이 있다고 하면,

$$(6 + 5) \times 2 - 9 \div 3 \times ((7 + 5) \div (9 - 3))$$

식을 다음과 같은 트리 형태로 나타낼 수 있다.

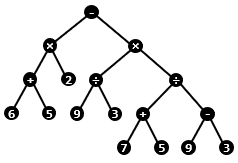
이 트리를 전위 순회한 결과는 다음과 같다.

$$- \times + \ 6 \ 5 \ 2 \times \div \ 9 \ 3 \div + \ 7 \ 5 - 9 \ 3$$

이런 형태의 식을 전위 표기식(Prefix Expression)이라고 하며 식을 이 방법으로 나타내는 것을 전위 표기법(Prefix Notation) 또는 폴란드 표기법(Polish Notation, PN)이라고 한다.

---

1. 깊이 우선 순회(Depth First Traversal)라는 용어가 동의어로 존재하지만 거의 쓰이지 않는 것 같다. [본문으로]