트리의 지름은 다음과 같이 정의된다.
- 트리에 존재하는 임의의 정점 $u$와 $v$에 대해, 두 정점 사이에는 항상 한 개의 단순 경로가 존재하며 이 단순 경로의 길이를 정점 $u$와 $v$ 사이의 거리(Distance)라고 한다.
- 트리의 한 정점 $u$과 임의의 정점 $v$에 대해, 정점 $u$와 $v$ 사이의 거리의 최대값을 정점 $u$에서의 이심률(Eccentricity)이라고 한다.
- 트리의 각 정점에서의 이심률의 최소값을 트리의 반지름(Radius of Tree)이라고 하고 이심률의 최대값을 트리의 지름(Diameter of Tree)이라고 한다.
쉽게 말해서 트리의 지름은 트리에 존재하는 두 정점 사이의 거리의 최대값과 같다. 위 용어들 중에서 이심률은 볼 일이 거의 없으므로 몰라도 무방하지만 나머지 용어들은 자주 쓰이므로 알아 두어야 한다.
다음과 같은 트리에서 지름은 $4$, 반지름은 $2$이다.

간선에 가중치가 생겨도 트리의 지름과 반지름의 정의는 달라지지 않는다. 다음과 같은 트리에서 지름은 $17$(정점 $\text{A}$와 $\text{D}$ 사이의 거리), 반지름은 $10$(정점 $\text{B}$)이 된다.

트리의 지름을 구하는 가장 간단한 방법은 다음과 같다.
- 트리에서 아무 정점이나 하나를 선택하고 그 정점에서 가장 거리가 먼 정점 $u$를 찾는다. 가장 거리가 먼 정점이 여러 개일 경우 아무거나 하나를 선택한다.
- 정점 $u$에서 가장 거리가 먼 정점 $v$를 찾는다. 트리의 지름은 정점 $u$와 $v$ 사이의 거리와 같다.
이 방법은 임의의 정점에서 가장 먼 정점을 한쪽 끝점으로 하는 트리의 지름이 항상 존재한다는 사실을 기반으로 한다. 이 사실은 다음과 같이 증명할 수 있다.
${\color{#FF0000}{[1]}}$ 트리의 어떤 정점 $p$에서 가장 먼 정점 중의 하나가 $u$이고, 정점 $u$를 한쪽 끝점으로 하는 트리의 지름이 존재하지 않는다고 가정한다.
${\color{#FF0000}{[2]}}$ 트리의 지름은 어떤 두 정점 사이의 경로의 단순 길이와 같으므로 이 두 정점을 각각 $v_1$, $v_2$라고 할 수 있다. 또한 정점 $v_1$, $v_2$ 사이의 단순 경로상에 존재하는 정점들 중 $u$와 가장 거리가 가까운 정점을 $a$라고 하고 정점 $p$, $u$ 사이의 단순 경로상에 존재하는 정점들 중 $a$와 가장 거리가 가까운 정점을 $b$라고 하자.
${\color{#FF0000}{[3]}}$ 정점 $x$와 정점 $y$ 사이의 거리를 $d(x, y)$로 정의하면 트리의 지름은 $d(v_1, v_2)$라고 할 수 있다. 또한 $[2]$에 의해 $d(v_1, v_2) = d(v_1, a) + d(a, v_2)$이고 $d(p, u) = d(p, b) + d(b, u)$이다.
${\color{#FF0000}{[4]}}$ $u$가 $p$에서 가장 먼 정점 중의 하나이므로 $d(p, u) \ge d(p, v_1)$이다. 또한 $d(p, v_1) = d(p, b) + d(b, a) + d(a, v_1)$이다.
${\color{#FF0000}{[5]}}$ $[3]$, $[4]$에 의해 $d(p, b) + d(b, u) \ge d(p, b) + d(b, a) + d(a, v_1)$이고, 양변에서 $d(p, b)$를 빼면 $d(b, u) \ge d(b, a) + d(a, v_1)$이다.
${\color{#FF0000}{[6]}}$ $[5]$의 마지막 식의 양변에 $d(b, a)$를 더하면 $d(b, u) + d(b, a) \ge 2d(b, a) + d(a, v_1)$이고, $d(b, a) \ge 0$이므로 $d(b, u) + d(b, a) \ge d(a, v_1)$이다.
${\color{#FF0000}{[7]}}$ 정점 $b$, $u$ 사이의 단순 경로와 정점 $b$, $a$ 사이의 단순 경로가 간선을 공유하지 않기 때문에 $d(b, u) + d(b, a) = d(a, u)$이다. 따라서 $d(a, u) \ge d(a, v_1)$이고, 양변에 $d(a, v_2)$를 더하면 $d(a, u) + d(a, v_1) \ge d(a, v_2) + d(a, v_1) = d(v_1, v_2)$이다.
${\color{#FF0000}{[8]}}$ 정점 $a$, $u$ 사이의 단순 경로와 정점 $a$, $v_1$ 사이의 단순 경로가 간선을 공유하지 않기 때문에 $d(a, u) + d(a, v_1) = d(v_1, u)$이다. 따라서 $d(v_1, u) \ge d(v_1, v_2)$이다.
${\color{#FF0000}{[9]}}$ $d(v_1, v_2)$를 트리의 지름이라고 가정했으므로 $d(v_1, u) \le d(v_1, v_2)$이다.
${\color{#FF0000}{[10]}}$ $[8]$, $[9]$에 의해 $d(v_1, u) = d(v_1, v_2)$이고, 이것은 정점 $u$와 $v_1$ 사이의 거리가 트리의 지름과 같다는 의미이므로 $[1]$과 모순된다. 따라서 $[1]$의 가정이 잘못되었음을 확인할 수 있다.
정점의 배치를 그림으로 나타내면 다음과 같다.

정점 $a$와 정점 $b$가 일치해도 위의 증명 방법은 유효하다.
따라서 이 방법으로 트리의 지름을 구할 수가 있다. 구현은 다음과 같이 단순 DFS $2$번으로 가능하다.
#import<bits/stdc++.h>
using namespace std;
int m, d[100005];
vector<int>e[100005];
void dfs(int prev, int node)
{
if(d[node] > d[m])m = d;
for(auto &p: e[node])
{
if(p != prev)
{
d[p] = d[node] + 1;
dfs(node, p);
}
}
}
int main()
{
int n, x, y;
cin >> n;
for(int i = 1; i < n; i++)
{
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(0, 1);
fill(d, d + n + 1, 0);
dfs(0, m);
}두 번의 DFS 실행이 끝난 후 $d[m]$에 트리의 지름이 저장된다. 이 방법을 사용하면 트리의 반지름도 쉽게 구할 수 있다. 이번에는 트리의 반지름이 항상 트리의 지름에 포함된다는 것을 증명해야 하는데, 증명 과정은 다음과 같다.
${\color{#FF0000}{[1]}}$ 두 정점 $v_1$, $v_2$ 사이의 단순 경로의 길이가 트리의 지름이고 이 단순 경로에 포함되지 않는 정점 $p$가 존재한다고 가정한다. (만약 정점 $p$가 존재하지 않을 경우 트리가 일자형이므로 트리의 반지름은 트리의 지름에 포함된다.)
${\color{#FF0000}{[2]}}$ 정점 $x$와 정점 $y$ 사이의 거리를 $d(x, y)$로 정의하고, 정점 $v_1$, $v_2$ 사이의 단순 경로상에 존재하는 정점들 중 $p$와 가장 거리가 가까운 정점을 $a$라고 하자. 이때 일관성을 위해 $d(a, v_1) \ge d(a, v_2)$라고 가정한다.
${\color{#FF0000}{[3]}}$ 또 다른 정점 $u$가 존재한다고 가정한다. 이때 정점 $a$, $p$ 사이의 단순 경로와 정점 $p$, $u$ 사이의 단순 경로가 간선을 공유하지 않아야 하고, 정점 $p$와 $u$ 사이의 거리가 최대가 되어야 한다.
${\color{#FF0000}{[4]}}$ 정점 $x$와 정점 $y$ 사이의 거리를 $d(x, y)$로 정의하면 $[3]$에 의해 $d(a, u) = d(a, p) + d(p, u)$이고, d(v_1, v_2) = d(v_1, a) + d(a, v_2)$이다.
${\color{#FF0000}{[5]}}$ $d(v_1, v_2)$가 트리의 지름이므로 $d(v_1, v_2) \ge d(v_1, u)$이고, 정점 $v_1$, $a$ 사이의 단순 경로와 정점 $a$, $u$ 사이의 단순 경로가 간선을 공유하지 않으므로 $[4]$에 의해 $d(v_1, a) + d(a, v_2) \ge d(v_1, a) + d(a, u)$이다. 양변에서 $d(v_1, a)$를 빼면 $d(a, v_2) \ge d(a, u)$이다.
${\color{#FF0000}{[6]}}$ $[2]$, $[5]$에 의해 $d(a, v_1) \ge d(a, v_2) \ge d(a, u)$이다. 양변에 $d(a, p)$를 더하면 $d(p, v_1) \ge d(p, v_2) \ge d(a, u) + d(a, p) = d(p, u) + 2d(a, p)$이다. 따라서 $d(p, v_1) \ge d(p, v_2) \ge d(p, u)$이다.
${\color{#FF0000}{[7]}}$ $[6]$에 의해 정점 $p$에서의 이심률은 $d(p, v_1)$이 되는데, 확인해 보면 정점 $p$에서 가장 먼 정점이 $v_1$이 아닐 경우 트리의 지름이 $d(v_1, v_2)$라는 사실과 모순이 된다는 것을 알 수 있다. (자세한 내용은 생략했다)
${\color{#FF0000}{[8]}}$ 정점 $p$, $a$ 사이의 단순 경로상에 존재하고 $p$와 인접한 정점 $q$가 존재한다고 하면, 정점 $p$를 $q$로 대체한 다음 $[3]$부터 $[6]$까지의 단계를 반복했을 때 정점 $q$에서의 이심률이 $d(q, v_1)$임을 확인할 수 있다. 이때 $d(p, v_1) \ge d(q, v_1)$이므로 정점 $p$를 $q$로 대체했을 때 이심률은 증가하지 않는다.
${\color{#FF0000}{[9]}}$ $[7]$과 같은 방식으로 정점을 계속해서 대체하면 언젠가는 정점 $p$가 정점 $a$와 같아지게 된다. 이때 트리의 반지름은 $d(a, v_1)$과 같으므로 트리의 지름에 포함된다. 따라서 처음에 어떤 정점을 $p$로 선택하더라도 트리의 반지름이 트리의 지름에 포함된다는 결론을 얻는다.
정점의 배치를 그림으로 나타내면 다음과 같다.

따라서 트리의 지름상에 존재하는 정점들 중 이심률이 최소가 되는 정점을 찾으면 트리의 반지름을 구할 수 있다. 이심률을 구할 때는 지름의 양 끝까지의 거리만 확인하면 된다.
위에서 설명한 방법은 트리의 지름과 반지름을 간단하게 구하는 데 효과적이지만, 트리에 가중치가 음수인 간선이 있으면 써먹을 수가 없다는 문제점이 존재한다. 이런 경우는 트리 DP를 이용하면 트리의 지름을 구할 수 있다. 기본적인 방법은 다음과 같다.
- 임의의 정점을 루트로 잡고, 각각의 노드에 대해 각각의 자식 노드를 루트로 하는 서브트리에 속한 정점까지의 거리의 최대값을 구한다.
- 구한 값을 바탕으로 트리의 지름을 구한다.
설명이 별로 간단하지 않으므로 예시를 살펴보자. 다음과 같은 트리에서 지름은 $5$이다. 이것은 정점 $\text{A}$와 $\text{F}$ 사이의 거리인데, 지름의 한쪽 끝인 $\text{A}$가 리프 노드가 아니다. 이것은 가중치가 음수인 간선이 있어서 생기는 현상이며, 간선의 가중치가 모두 $0$ 이상인 트리에서는 두 리프 노드 사이의 거리가 트리의 지름이 되는 경우가 반드시 존재한다.

현재 노드 $\text{I}$가 루트 노드로 선택되었다. 여기서 DFS를 실행하면서 DP 테이블을 채운다. 실행이 끝나면 DP 테이블은 빨간색으로 표시된 값으로 채워진다. (중간 과정은 생략함)

여기서 트리에 존재하는 단순 경로의 특징을 살펴보면, 노드에서 계속 부모 노드로 올라가다가 어느 순간부터 계속 자식 노드로 내려가는 형태라는 것을 확인할 수 있다. 또한 어떤 경로는 계속 자식 노드로 내려가기만 한다. 이 전환점의 DP 테이블에 채워진 값을 확인하면 트리의 지름을 구할 수 있게 된다. 각각의 노드에 대해 $\max($자식 노드 쪽의 DP 테이블에 채워진 가장 큰 값$,$ 자식 노드 쪽의 DP 테이블에 채워진 가장 큰 두 값의 합$,$ $0)$을 구한 다음 다시 그 값의 최대값을 구하면 트리의 지름이 나온다.
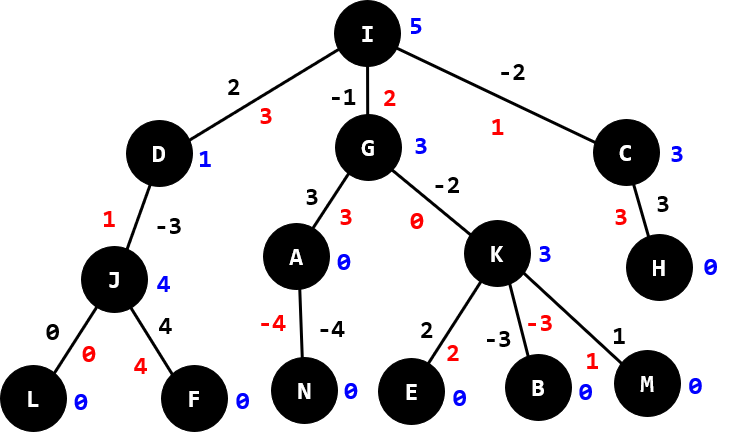
값이 많으므로 주의해서 읽어야 한다. 파란색으로 표시된 값 중 최대값이 트리의 지름이다.
구현은 다음과 같다.
#import<bits/stdc++.h>
using namespace std;
int m, d[100005];
vector<int>e[100005];
void dfs(int prev, int node)
{
int x = 0, y = 0;
for(auto &p: e[node])
{
if(p != prev)
{
dfs(node, p);
if(d[p] > x)
{
y = x;
x = d[p];
}
else if(d[p] > y)y = d[p];
}
}
d[node] = x + y;
m = max(m, d[node]);
}
int main()
{
int n, x, y;
cin >> n;
for(int i = 0; i < n - 1; i++)
{
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(0, 1);
}트리의 지름을 구하기 위한 DFS에서는 자식 노드의 DP 값 중 가장 큰 두 개의 정보만 저장해도 되므로 위와 같이 $x$, $y$ 두 개의 변수로 이 값들을 저장하는 식으로 구현해도 된다. DFS의 실행이 끝난 후 $m$이 트리의 지름이 된다.
이 방법은 가중치가 음수인 간선이 있는 경우에도 잘 작동하지만 한 가지 사소한 문제가 있다. 만약 간선의 가중치가 모두 음수라면 DFS 결과 트리의 지름은 $0$으로 계산되는데, 이것은 간선을 한 개도 지나지 않는 경로이므로 어떤 상황에서는 경로로 간주하기 애매할 수 있다. 만약 이런 상황에서 간선을 한 개 이상 지나는 것만 경로로 간주할 경우 간선의 가중치의 최대값을 찾으면 그 값이 트리의 지름이 된다.
[연습문제]
가중치가 있는 트리의 지름을 구한다.
가중치가 있는 트리의 지름을 구한다. 입력 형식이 1967번과 조금 다르다.
'Algorithm > H. Trees & Graphs' 카테고리의 다른 글
| 115. Dijkstra (0) | 2022.02.25 |
|---|---|
| 114. Shortest Path (0) | 2021.12.30 |
| 112. Bipartite Graph (0) | 2021.12.27 |
| 111. Grid & Flood Fill (0) | 2021.12.25 |
| 110. Breadth First Search (0) | 2021.12.22 |



