이번에 다루는 내용은 트리 구조를 응용한 것이다.
집합론에서 분리 집합(Disjoint Set)은 공통 원소가 없는 두 집합을 의미한다. 컴퓨터과학에서 이 개념은 한 개 이상의 집합으로 확장되며, 한 개의 집합 또는 어떤 두 집합도 공통 원소를 갖지 않는 두 개 이상의 집합을 분리 집합이라고 생각하면 된다. $0$개의 집합 같은 경우는 생각하지 않는다.
분리 집합은 아래의 두 가지 연산에 의해서 여러 활용도를 갖게 된다.
- 두 집합을 하나로 합친다. (Union)
- 원소가 현재 어떤 집합에 속해 있는지 확인한다. (Find)
이 두 연산의 이름을 따서 유니온-파인드(Union-Find)라는 이름이 생겨났다.
이 개념을 PS의 관점에서 보면, 일단 각각의 집합은 서로 구별이 가능한 식별자를 갖고 있어야 한다. 일반적으로 $n$개의 원소가 존재할 때 집합도 $n$개가 존재한다고 가정하고 각각에 $1$번부터 $n$번까지 식별자를 부여한다. $i$번 원소는 $i$번 집합에 존재한다. 이렇게 초기화를 하고, 초기 상태에 이미 서로 합쳐진 집합들이 존재한다면 Union 연산으로 전처리를 해 주면 된다.
#import<bits/stdc++.h>
using namespace std;
int p[100005]; // p는 parents의 약자로 사용됨
int main()
{
int n;
cin >> n;
iota(p, p + n + 1, 0);
}std::iota 함수는 메모리의 시작 위치 $s$, 끝 위치 $e$와 초기값 $v$를 인자로 받아서 구간 $[s, e)$에 속하는 원소들의 값을 $v, v+1, v+2, \ldots, v+e-s-1$로 바꾼다.
$p[i]$는 $i$번 원소가 속한 집합을 나타내는 배열이다. 그런데 이것은 정점이 $1$개인 트리 $n$개가 존재하는 것으로도 해석할 수 있다.
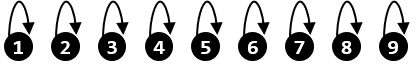
그림으로 나타내면 이렇게 된다. 화살표는 $i$와 $p[i]$의 관계를 표시한 것으로, 초기에는 모든 $i$에 대해 $p[i] = i$로 초기화되기 때문에 모든 화살표가 자신에게 되돌아온다. 또한 각각의 트리에 정점이 하나밖에 없기 때문에 이 상태에서는 각각의 정점이 전부 트리의 루트이다.
이 관점에서 Union과 Find 연산을 해석한다면, Union 연산은 두 트리를 합치는 것이므로 한쪽 트리의 루트를 다른 트리의 서브트리로 만드는 것과 같고, Find 연산은 어떤 정점이 속한 트리의 루트를 찾는 것과 같다. $i$번 정점이 루트인 트리를 $i$번 트리라고 부르고, 두 정점을 한 집합으로 합칠 때 두 정점이 속한 집합이 전부 하나로 합쳐진다고 할 때, $1$번 정점과 $2$번 정점을 한 집합으로 합치면 다음과 같이 된다.
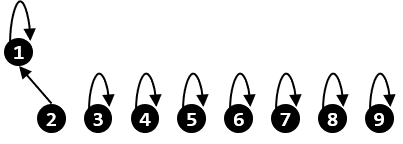
$p[2]$가 $1$로 바뀌었다. 다음으로 $3$번 정점과 $5$번 정점을 합치고, $6$번 정점과 $7$번 정점을 합친다.
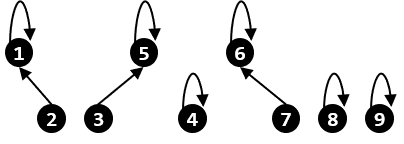
만약 여기서 $3$번 정점과 $6$번 정점을 합치는 상황이 발생한다면, 일단 두 정점이 속한 트리의 루트를 찾은 다음 한쪽 루트를 다른 쪽 루트의 자식으로 연결한다.

또한 $5$번 정점과 $7$번 정점을 합치는 상황이 발생할 경우, 두 정점이 이미 같은 집합에 속해 있기 때문에 아무것도 하지 않아도 된다.

이렇게 여러 개의 트리 구조로 집합을 표현하면 Union과 Find 연산은 일단 사용이 가능하게 된다. 구현은 이렇게 되는데, union은 일부 언어에서는 식별자라서 함수 이름에 쓸 수 없고, find 역시 std::find 등과 이름이 충돌할 가능성이 있다. 따라서 겹치지 않는 적절한 이름을 선택하는 것이 필요하다. 이 블로그에서는 _union, _find로 대체하였다.
void _union(int x, int y)
{
while(x != p[x])x = p[x];
while(y != p[y])y = p[y];
p[y] = x;
}
int _find(int x)
{
while(x != p[x])x = p[x];
return x;
}위에서 제시한 방법은 최적화를 아무것도 하지 않기 때문에, Union 연산이나 Find 연산을 한 번 실행하는 데 걸리는 시간은 $O(n)$이다. 처음 상태로 되돌아가서, $1$번 정점과 $2$번 정점을 합치고, $2$번 정점과 $3$번 정점을 합치고, 같은 방법으로 $9$번 정점까지 모두 합친 상태를 생각해 보자.
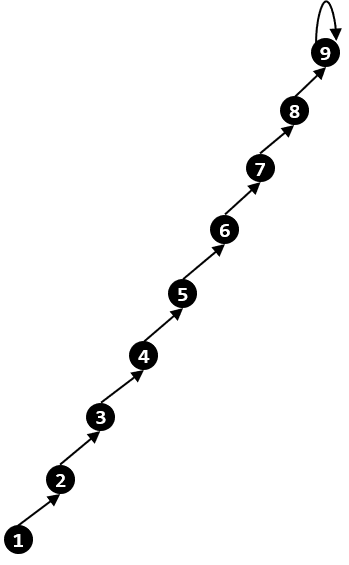
트리를 합치는 방법에 따라 이런 트리가 생길 수도 있다. 이 상태에서 $1$번 정점이 속한 집합을 확인하려면, $1$번 정점에서 시작해서 부모 정점으로 이동하는 과정을 반복하면서 $2$번 정점부터 $9$번 정점까지를 차례로 지나가고 나서야 $1$번 정점이 $9$번 집합에 존재한다는 것을 알 수 있게 된다. 따라서 원소의 수가 $n$, 연산 횟수가 $m$일 때 모든 연산을 처리하는 시간은 $O(nm)$이 된다. $n$과 $m$이 $10$만 정도로 커진다면 너무 느려서 이대로는 써먹을 수가 없다.
이런 문제점을 해결하기 위해 두 가지 방법이 고안되었다. 첫 번째는 랭크에 의한 합치기(Union by Rank)로, 트리의 대략적인 높이를 저장한 다음 높이가 낮은 트리를 높이가 높은 트리의 자식으로 연결하는 것이다. 초기 상태에서 트리의 높이는 전부 $0$이다.
이 방법으로 위에 나온 과정을 실행하면 트리는 이런 모양이 되며, 높이가 $8$에서 $1$로 줄어들었다.
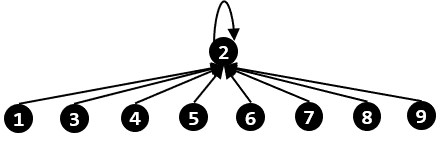
이 방법의 시간복잡도를 분석해 보면, 높이가 $x$인 트리는 높이가 $(x - 1)$인 두 트리를 합칠 때만 새로 생겨난다. 따라서 높이가 $x$인 트리에 존재하는 정점의 최소 개수를 $f(x)$라고 하면 $f(x) = 2f(x - 1)$이 성립한다. $f(0) = 1$이므로 $f(x) = 2^x$가 되며, 이로부터 랭크에 의한 합치기를 적용했을 때 정점이 $n$개인 트리의 높이는 $\lg n$을 넘지 않음을 알 수 있다. 따라서 $m$번의 연산을 처리하는 시간이 $O(m \lg n)$으로 줄어든다. 하지만 뒤에 소개하는 방법이 성능이 더 좋기 때문에 일반적인 Union-Find 문제에서는 이 방법을 쓸 일이 별로 없다.
두 번째 방법은 경로 압축(Path Compression)으로, 트리에서 루트로 이동하는 과정에서 지나가는 정점들의 부모 정점을 모두 루트로 바꿔주는 방식이다. 이 방법을 사용하면 트리의 높이가 잠시 높아지더라도 큰 문제가 되지 않는다. 위의 과정을 실행하는 경우를 다시 생각해 보면, 일단 랭크에 의한 합치기 방법은 적용하지 않기 때문에 트리의 높이가 $8$이 될 수 있다.
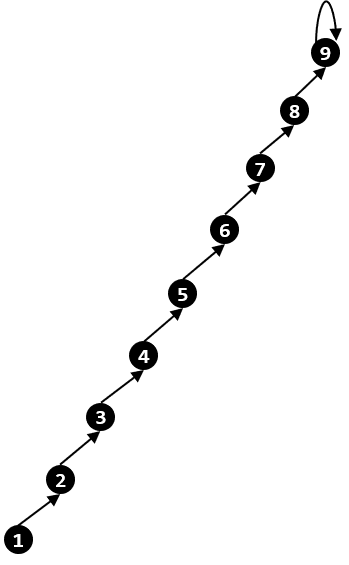
이 상태에서 $4$번 정점이 속한 집합을 확인한다면 $4$번 정점부터 $9$번 정점까지를 차례로 지나가게 되는데, 이때 이 정점들의 부모 정점을 모두 $9$번 정점으로 바꾼다. 그러면 트리의 높이는 $3$으로 낮아진다.
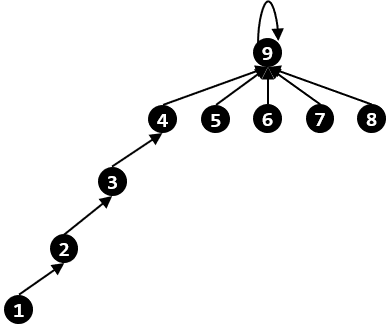
이 상태에서 다음에 다시 $4$번 정점이 속한 집합을 확인하더라도 $4$번 정점과 $9$번 정점만을 지나가므로 효율성이 높아짐을 알 수 있다.
경로 압축을 사용했을 때 $m$번의 연산을 처리하는 시간은 일반적으로 $O(m \alpha(n))$으로 표기한다. $\alpha(n)$은 애커만 함수의 역함수로 매우 느리게 증가하며, 문제 해결에서 나올 수 있는 모든 $n$에 대해 $\alpha(n) < 5$를 만족한다고 가정해도 된다. 그렇다면 $\alpha(n)$은 사실상 상수와 같으며, 이후의 글들에서는 이것을 상수 시간에 실행되는 것으로 간주할 것이다.
일반적으로 여기까지가 유니온-파인드의 기본적인 내용이다. 구현은 다음과 같이 할 수 있는데 다른 방식도 많이 존재하므로 편한 구현을 찾아서 쓰면 된다.
int _union(int x, int y)
{
if(x != p[x] || y != p[y])return p[x] = p[y] = _union(p[x], p[y]);
return p[y] = x;
}
int _find(int x)
{
if(x != p[x])return p[x] = _find(p[x]);
return x;
}유니온-파인드는 꽤 다양하게 응용할 수 있다.
먼저 집합의 크기를 구해야 하는 경우, 트리의 루트 노드마다 트리에 속한 정점 수를 저장한 다음 Union 연산 시 갱신해 주면 된다. 기본 코드에서 조금만 추가하면 된다.
#import<bits/stdc++.h>
using namespace std;
int p[100005], sz[100005]; // sz는 size의 약자로 사용됨
int _union(int x, int y)
{
if(x != p[x] || y != p[y])return p[x] = p[y] = _union(p[x], p[y]);
sz[x] += sz[y];
return p[y] = x;
}
int _find(int x)
{
if(x != p[x])return p[x] = _find(p[x]);
return x;
}
int main()
{
int n;
cin >> n;
iota(p, p + n + 1, 0);
fill(sz + 1, sz + n + 1, 1);
}또 어떤 문제들에서는 정점들이 두 그룹 중 하나에만 속할 수 있고, 두 정점이 서로 같은 그룹에 속한다는 정보 또는 서로 다른 그룹에 속한다는 정보들이 주어진다. 이것도 유니온-파인드로 처리할 수 있으며, 각각의 정점에 대해 '그 정점과 다른 그룹에 속하는 정점'을 나타내는 가상의 정점들을 추가하면 구현이 간단해진다. 정점 $(n+k)$가 정점 $k$와 다른 그룹에 속하는 정점을 나타낸다고 하면, 다음과 같이 처리가 가능하다.
- 정점 $x$와 $y$가 같은 그룹에 속한다는 정보가 주어진 경우: $\text{Union}(x, y), \text{Union}(n + x, n + y)$
- 정점 $x$와 $y$가 다른 그룹에 속한다는 정보가 주어진 경우: $\text{Union}(x, n + y), \text{Union}(n + x, y)$
만약 정점 $x$와 $(n + x)$가 같은 그룹에 속하게 된다면, 모순이 발생한 것이다. 또한 여기서 집합의 크기까지 알아야 한다면, $\text{sz}[1]$부터 $\text{sz}[n]$까지만 $1$로 초기화하면 된다. $(n + 1)$번 정점부터 $2n$번 정점까지는 가상의 정점이므로 집합의 크기를 늘리지 않는다.
[연습문제]
선분들을 Union 연산으로 그룹으로 묶는다. 만약 같은 그룹에 속한 선분들을 다시 묶게 되었다면 사이클이 생긴 것이다.
다리가 없는 상태에서 시작해서 중량 제한이 큰 다리부터 하나씩 설치하다가 두 공장이 서로 이어졌을 때 설치한 다리의 중량 제한이 답이 된다. 다리를 설치하는 것을 Union 연산으로 처리할 수 있다.
기본 유니온-파인트에 집합의 크기를 구하는 부분이 추가되었다. std::map을 써서 각각의 이름에 번호를 매긴 다음 구현하면 된다.
각각의 문명 발상지에서 시작해서 BFS로 인접한 지역에 문명을 전파하고, 두 문명이 인접한 경우 Union 연산으로 하나로 합치는 과정을 반복한다. 구현 시 미스가 나지 않도록 주의해야 한다.
$(M - 1)$번 도로부터 $0$번 도로까지를 차례로 확인하면서 $i$번 도로를 추가했을 때 $0$번 교차로와 $(N - 1)$번 교차로가 연결된다면 답에 $3^i$를 더한 다음 도로는 추가하지 않고, 아니면 그 도로를 추가하는 과정을 반복하면 된다.
BOJ 21210. Safe Distance (Platinum III)
왼쪽-위 가장자리와 오른쪽-아래 가장자리와 각각의 사람을 정점으로 간주하고, 그리드에서 두 정점 사이의 최단 거리를 그래프에서 두 정점을 잇는 간선의 가중치라고 간주한다. 이렇게 한 다음 가중치가 작은 간선부터 하나씩 추가하다가 두 가장자리를 나타내는 정점이 같은 그룹에 속하게 되었을 때 추가한 간선의 가중치의 절반이 답이 된다.
BOJ 21932. To be Connected, or not to be, that is the Question (Platinum I)
$x$ 이하의 값이 적힌 정점끼리 연결하는 간선과 $x$ 초과의 값이 적힌 정점끼리 연결하는 간선들만 남겼을 때 두 그룹에 각각 몇 개의 컴포넌트와 정점이 속하는지를 구해서 답을 내면 된다. 컴포넌트의 개수를 셀 때 유니온-파인드가 사용된다.
CF 1559D1. Mocha and Diana (Easy Version) (1400)
각각의 간선 쌍을 추가할 수 있는지 전부 확인하면 된다. 기본 문제에서 별로 추가된 게 없다.
'Algorithm > H. Trees & Graphs' 카테고리의 다른 글
| 126. Kruskal's Algorithm (0) | 2022.06.30 |
|---|---|
| 125. Minimum Spanning Tree (0) | 2022.06.24 |
| 123. Topological Sorting (0) | 2022.04.30 |
| 122. Directed Acyclic Graph (0) | 2022.04.29 |
| 121. Independent Set & Clique (0) | 2022.04.25 |



