다음과 같은 트리가 있다고 가정해 보자.

$9$번 정점이 루트라고 하면 다른 정점들의 부모와 조상들을 결정할 수 있다. 예를 들어 $3$번 정점의 부모는 $9$번 정점이고, $8$번 정점의 조상은 $5$번 정점과 $9$번 정점이 된다.
이제 여러 정점의 조상을 생각해 보자. $7$번 정점의 조상은 $4$번, $3$번, $9$번 정점이고 $6$번 정점의 조상은 $3$번, $9$번 정점이다. 여기서 $3$번과 $9$번 정점은 $6$번 정점의 조상이면서 $7$번 정점의 조상이다. 이런 정점들을 $7$번 정점과 $6$번 정점의 공통 조상(Common Ancestor)이라고 한다. 또한 이중 깊이가 가장 깊은 정점은 $3$번 정점인데, 이 정점을 $7$번 정점과 $6$번 정점의 최소 공통 조상(Lowest Common Ancestor, LCA)이라고 한다. 공통 조상과 최소 공통 조상은 같은 트리에 존재하는 두 개 이상의 정점들에 대해 잘 정의되며 여러 정점들의 최소 공통 조상은 항상 한 개 존재한다.
그러면 최소 공통 조상을 어떻게 구할 수 있는지 살펴보자. 블로그를 살펴보면 대부분 한 가지 방법만 소개하거나 나머지 방법을 간단하게만 소개하는데 여기서는 그러지 않는다.
가장 많이 알려진 방법은 희소 테이블을 이용하는 것이다. 어떤 정점에서 부모 정점으로 $x$번 이동했을 때 도착하는 정점을 그 정점의 $x$번째 조상이라고 하면(공식 용어는 아니다), 각각의 정점마다 $2^k$번째 조상을 희소 테이블에 저장하면1 다음과 같은 방법으로 두 정점의 최소 공통 조상을 구할 수 있다. 쉬운 설명을 위해 두 정점에 토큰이 하나씩 있다고 하자.
- 두 정점의 깊이가 다를 경우 깊이가 같아질 때까지 더 깊은 정점에 있는 토큰을 부모 정점으로 옮긴다.
- 토큰이 서로 다른 정점에 있을 경우 토큰이 한 정점에 모일 때까지 두 토큰을 동시에 각각의 부모 정점으로 옮긴다.
- 두 토큰이 놓인 정점이 두 정점의 최소 공통 조상이 된다.
만약 두 번째 과정을 실행하지 않았다면 한 정점이 다른 정점의 조상이거나 두 정점이 동일한 경우이다. 위에 나온 트리에서 $6$번 정점과 $7$번 정점의 최소 공통 조상을 구하는 경우를 다시 생각해 보자.

$7$번 정점의 깊이가 더 깊으므로 토큰을 부모 정점으로 옮기는 과정을 반복한다. 여기서는 $4$번 정점에 토큰이 놓이게 된다.

두 토큰이 아직 다른 정점에 있으므로 토큰을 동시에 부모 정점으로 옮기는 과정을 반복한다. 그러면 $3$번 정점에 두 토큰이 놓이게 된다.

따라서 $6$번 정점과 $7$번 정점의 최소 공통 조상이 $3$번 정점이라는 것을 알 수 있다. 이번에는 시간복잡도를 계산해 보자. 먼저 정점이 $n$개인 트리의 조상 정보를 담은 희소 테이블을 $O(n \lg n)$ 시간에 구축할 수 있고, 두 정점의 깊이를 알아내는 것은 입력 형식이나 구현 방식에 따라 약간의 차이가 있을 수 있지만 희소 테이블이 있는 이상 $O(\lg n)$ 시간에 할 수 있다. 만약 루트에서 DFS를 실행하면서 모든 정점의 깊이를 다 전처리했을 경우 $O(1)$ 시간에 알아낼 수도 있고, 두 정점의 최소 공통 조상을 여러 번 구해야 하는 경우 이쪽이 속도가 더 빠를 수도 있다.
다음으로 깊은 정점에 있는 토큰을 옮겨서 깊이가 같아지게 만드는 것은 $O(\lg n)$ 시간에 할 수 있다. 앞에서 구축한 희소 테이블을 이용하면 된다. 그리고 그 상태에서 두 토큰이 같은 정점에 오도록 하는 것도 $O(\lg n)$ 시간에 할 수 있는데, 다음과 같은 방법을 사용한다. 이분 탐색의 관점에서 이해하면 약간 더 알기 쉬울 것이다.
- $n$보다 작은 $2$의 거듭제곱 중 가장 큰 수를 $p$라고 하자. 두 정점의 $p$번째 조상이 서로 다른 경우 두 토큰을 각각의 $p$번째 조상으로 옮긴다. $p$번째 조상이 같은 경우 토큰을 옮기지 않는다.
- $p$를 $2$로 나누면서 각각의 $2$의 거듭제곱마다 위의 과정을 반복한다.
- $p = 1$까지 반복을 완료한 경우 두 토큰을 부모 정점으로 한번 더 옮긴다. 두 토큰이 놓인 정점이 두 정점의 최소 공통 조상이 된다.
즉 두 정점의 $x$번째 조상이 서로 다른 최대의 $x$를 찾는 것이다. 그렇게 해서 두 토큰을 형제 정점에 놓이게 하면 최소 공통 조상을 찾을 수 있다.
구현은 다음과 같다. 코드를 자세히 읽다 보면 의문점이 생길 수도 있는데, 연습문제 LCA 2의 설명에 관련된 내용을 정리하였다.
#import<bits/stdc++.h>
using namespace std;
int d[100005], st[17][100005];
vector<int> e[100005];
void dfs(int p, int u)
{
d[u] = d[p] + 1;
st[0][u] = p;
for(auto &v: e[u])
{
if(p != v)dfs(u, v);
}
}
int LCA(int x, int y)
{
if(d[x] > d[y])swap(x, y);
for(int k = 0; k < 17; k++)y = d[y] - d[x] & 1 << k ? st[k][y] : y;
for(int k; x != y;)
{
for(k = 1; st[k][x] != st[k][y];)k++;
x = st[k - 1][x];
y = st[k - 1][y];
}
return x;
}
int main()
{
int n, x, y;
cin >> n;
for(int i = 1; i < n; i++)
{
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(0, 1);
for(int i = 1; i <= 16; i++)
{
for(int j = 1; j <= n; j++)st[i][j] = st[i - 1][st[i - 1][j]];
}
}아마 이 방법이 대부분의 블로그에서 소개하는 내용일 것이다. 하지만 최소 공통 조상을 구하는 방법은 더 있다.
이번에는 오일러 투어 테크닉을 이용해서 최소 공통 조상을 구하는 방법을 살펴본다. 먼저 정점들의 번호를 다시 매겨 보자. (어느 쪽 자식을 먼저 탐색하는지에 따라 번호가 조금씩 달라질 수 있지만 상관없다.)

이때 DFS 시 '거치는' 정점을 나열하면 다음과 같다.
$1 - 2 - 3 - 2 - 4 - 2 - 1 - 5 - 6 - 7 - 6 - 8 - 6 - 5 - 9 - 5 - 1 - 10 - 1$
이제 두 정점의 최소 공통 조상을 다음과 같은 방법으로 구할 수 있다.
- 새로 매긴 번호를 기준으로, 두 정점의 번호 중 가장 먼저 등장하는 것과 가장 나중에 등장하는 것의 위치를 찾는다.
- 찾은 위치에 해당하는 구간에서 등장하는 가장 작은 번호를 찾는다.
- 찾은 번호에 해당하는 정점이 두 정점의 최소 공통 조상이 된다.
처음 트리에서 $5$번과 $3$번 정점의 최소 공통 조상을 구하는 경우를 생각해 보자. 이 정점들은 번호를 다시 매긴 후에 각각 $2$번과 $5$번을 받았다.

앞에서 DFS 시 거치는 정점의 순서를 나열했을 때 $2$나 $5$가 처음으로 나오는 위치와 마지막으로 나오는 위치는 다음과 같다.
$1 - \color{#ff0000}2 - 3 - 2 - 4 - 2 - 1 - 5 - 6 - 7 - 6 - 8 - 6 - 5 - 9 - \color{#ff0000}5 - 1 - 10 - 1$
이제 이 구간에서 등장하는 가장 작은 번호를 찾는다. 여기서는 $1$이 가장 작은 번호가 된다.
$1 - \color{#ff0000}{2 - 3 - 2 - 4 - 2\ -} \color{#0000ff}{\ 1} \color{#ff0000}{ - 5 - 6 - 7 - 6 - 8 - 6 - 5 - 9 - 5} - 1 - 10 - 1$
즉 새로 매긴 번호를 기준으로 $1$번 정점이 두 정점의 최소 공통 조상이 된다. $1$번 정점의 원래 번호는 $9$번이므로 처음 트리에서 $5$번과 $3$번 정점의 최소 공통 조상은 $9$번 정점이 된다.
이 방법은 구현이 크게 두 가지로 갈린다. 첫 번째는 세그먼트 트리를 사용하는 방법으로 다음과 같이 구현할 수 있다.
#import<bits/stdc++.h>
using namespace std;
int c, p = 1 << 18, a[1 << 19], l[1 << 19], r[1 << 19], r1[100005], r2[100005], rinv[200004];
vector<int> e[100005];
void dfs(int pv, int u)
{
r1[u] = ++c;
rinv[c] = u;
a[p + c] = r1[u];
for(auto &v: e[u])
{
if(pv != v)
{
dfs(u, v);
a[p + (++c)] = r1[u];
}
}
r2[u] = c;
}
int getMin(int x, int y, int d)
{
if(x <= l[d] && r[d] <= y)return a[d];
if(x > r[d] || y < l[d])return 1 << 30;
return min(getMin(x, y, d << 1), getMin(x, y, d << 1 | 1));
}
int LCA(int x, int y)
{
return rinv[getMin(min(r1[x], r1[y]), max(r2[x], r2[y]), 1)];
}
int main()
{
int n, x, y;
cin >> n;
for(int i = 1; i < n; i++)
{
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
fill(a, a + p + p, 1 << 30); // INF로 초기화
dfs(0, 1);
for(int i = 0; i < p; i++)l[p + i] = r[p + i] = i;
for(int i = p; --i;)
{
l[i] = l[i << 1];
r[i] = r[i << 1 | 1];
a[i] = min(a[i << 1], a[i << 1 | 1]);
}
}두 번째는 희소 테이블을 사용하는 방법이다. 희소 테이블을 다룬 글의 연습문제로 있었던 최솟값 문제의 풀이와 유사한 방식을 사용하는 것으로, 쿼리를 상수 시간에 처리할 수 있다는 점 때문에 $\color{#FF0000}{O(1)}$ LCA라는 이름으로 불리기도 한다. 다음과 같이 구현할 수 있다.
#import<bits/stdc++.h>
using namespace std;
int c, lg[200004], r1[100005], r2[100005], rinv[200004], st[18][200004];
vector<int> e[100005];
void dfs(int p, int u)
{
r1[u] = ++c;
rinv[c] = u;
st[0][c] = r1[u];
for(auto &v: e[u])
{
if(p != v)
{
dfs(u, v);
st[0][++c] = r1[u];
}
}
r2[u] = c;
}
int LCA(int x, int y)
{
int rx = min(r1[x], r1[y]), ry = max(r2[x], r2[y]);
int p = lg[ry - rx + 1] - 1;
return rinv[min(st[p][rx], st[p][ry - (1 << p) + 1])];
}
int main()
{
int n, x, y;
cin >> n;
for(int i = 1; i < n; i++)
{
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
fill(st[0], st[0] + n + n, 1 << 30);
dfs(0, 1);
for(int i = 1; i <= 17; i++)
{
for(int j = 1; j <= 2 * n - (1 << i); j++)st[i][j] = min(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
}
for(int i = 1; i < 2 * n; i++)lg[i] = lg[i >> 1] + 1;
}
최소 공통 조상을 잘 사용하면 경로 쿼리 일부를 처리할 수도 있고, 분리 집합과 같이 사용하면 거의 모든 병렬 이분 탐색을 대체할 수도 있다.
[연습문제]
BOJ 11438. LCA 2 (Platinum V) [샘플 코드 1] [샘플 코드 2] [샘플 코드 3]
LCA 기본 문제이다. 각각의 샘플 코드는 위에서 소개한 세 가지 방법으로 구현한 것이다. 그런데 누군가는 샘플 코드 1에서 수상한 부분을 발견했을 것이다.
- 깊이가 같은 두 정점의 최소 공통 조상을 구하는 부분: 샘플 코드 1의 $18$~$23$행은 본문의 설명과는 약간 다르게 구현되어 있다. 둘 다 맞는 코드이므로 어떻게 구현해도 상관은 없다. 구현이 약간 달라진 이유는 단지 이쪽이 실행 시간이 더 짧게 나와서이다.
- 희소 테이블의 행 수: 샘플 코드 1에서 왜 희소 테이블이 $17$행밖에 되지 않는지 의문을 가지는 사람들이 있을 것이다. 희소 테이블이 $17$행까지 있다면 정점마다 $2^0$, $2^1$, $\ldots$, $2^{16}$번째 조상을 저장할 것이다. 이때의 의문점은 샘플 코드 1의 $20$행에서 희소 테이블 밖의 메모리를 참조하는 상황이 생길 수 있는가이다. 잘 생각해 보면, $17$행에서 두 정점의 깊이가 같아졌으므로 두 정점과 최소 공통 조상의 깊이 차이는 $N/2$를 넘지 않는다. $N$이 최대 $10^5$이므로 두 정점의 $2^{16}$번째 조상은 둘 다 존재하지 않으므로 희소 테이블에 저장된 값은 같아야 한다. 따라서 $20$행의 반복문에서 $k$는 $16$보다 커지지 않고, 희소 테이블 밖의 메모리를 참조하는 상황도 발생하지 않는다.
따라서 샘플 코드 1은 잘 작동하는 코드가 맞다.
BOJ 1761. 정점들의 거리 (Platinum V)
LCA로 처리할 수 있는 대표적인 쿼리로 두 정점의 최소 공통 조상을 구한 다음 깊이 차이를 구하면 두 정점 사이의 거리를 구할 수 있다. 그런데 이 문제는 $NM$이 최대 $4$억이라서 $O(NM)$ 풀이가 통과한다. 이것도 구현해 보도록 하자.
BOJ 3176. 도로 네트워크 (Platinum IV)
희소 테이블에 정점 번호뿐 아니라 도로 길이의 최솟값/최댓값도 저장하면 된다.
BOJ 13511. 트리와 쿼리 2 (Platinum III)
$1$번 쿼리는 희소 테이블에 비용 합을 저장하면 처리할 수 있고, $2$번 쿼리는 두 정점의 최소 공통 조상을 구한 다음 두 정점 중 한 정점에서 부모 정점으로 적당히 이동하면 처리할 수 있다.
BOJ 15480. LCA와 쿼리 (Platinum II)
일단 아무 정점이나 하나를 루트로 잡고 희소 테이블을 채운다. 그러면 $\text{LCA}(r, u)$, $\text{LCA}(r, v)$, $\text{LCA}(u, v)$ 중 가장 깊은 정점이 쿼리의 답이 된다. 또한 저 세 값들 중에 같은 값 두 개가 항상 존재하고, 나머지 하나를 골라도 답이 된다. 왜 그런지는 각자 확인해 보도록 하자.
BOJ 1396. 크루스칼의 공 (Platinum I)
최소 공통 조상과 분리 집합을 사용하는 문제이다. 먼저 간선을 고유값이 낮은 순서대로 정렬한 다음 간선을 하나씩 보면서 해당 간선이 두 정점을 직접 연결하는 게 아니라 새로운 정점이 있고 그 정점이 원래 간선이 연결하는 두 정점의 부모인 것으로 간주한다. 그리고 원래 간선의 고유값(빨간색)과 새로운 정점을 조상으로 하는 정점의 수(파란색)를 함께 저장한다. 예제에 나온 트리의 경우 이렇게 된다.
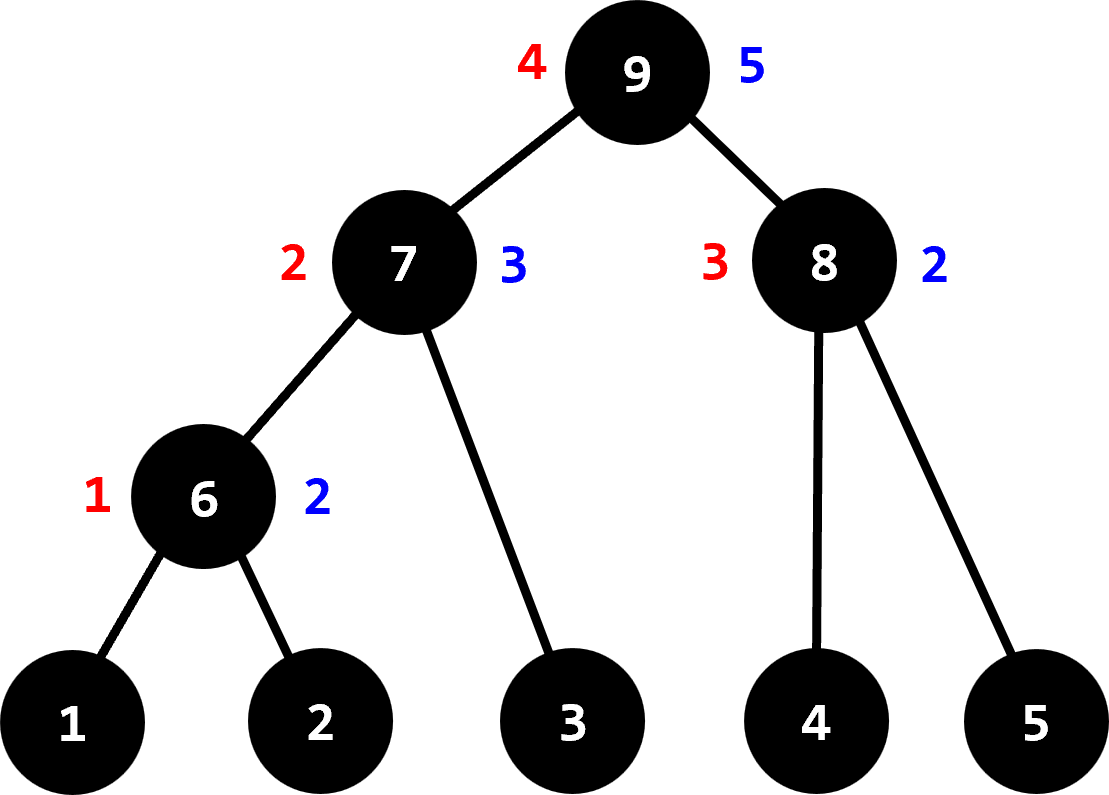
이제 입력되는 두 정점의 최소 공통 조상을 구하고 해당 정점에 저장된 빨간색과 파란색 값을 출력하면 된다. 예제 입력은 트리로 주어졌는데 문제의 조건에는 그래프가 입력된다고 명시되어 있으므로 불필요한 간선이 있을 수도 있고 연결 그래프가 아니라면 경로가 없어서 $-1$을 출력해야 할 수도 있다.
BOJ 1626. 두 번째로 작은 스패닝 트리 (Diamond IV)
꽤 유명한 문제인데 티어가 보여주듯 실수할 수 있는 부분이 많아서 주의해야 한다. 기본적인 아이디어는 최소 스패닝 트리에 포함되지 않는 간선들을 확인하면서 그 간선을 최소 스패닝 트리에 추가하고 기존에 있던 간선 하나를 제거했을 때 가중치의 합이 최소 스패닝 트리의 가중치보다는 크면서 최소가 되는 것을 찾는 것이다. 고리나 다중 간선도 입력될 수 있으므로 잘 처리하자.
포탈을 포함하면 한 개의 사이클이 있는 그래프가 생기므로 두 사람의 초기 위치에서 사이클까지의 거리와 사이클의 크기 등을 고려하여 열심히 케이스 처리를 하면 풀 수 있다. 이것도 중간에 LCA와 쿼리 문제에 등장하는 방법을 갖다 쓰고 누군가가 사이클에 도착하자마자 포탈을 통해 이동하는 경우, 포탈을 타고 이동할 때와 그렇지 않을 때의 손익 계산 등 여러 가지를 고려해야 한다.
BOJ 24835. 1-Trees and Queries (Platinum IV)
CF 1304E. 1-Trees and Queries (2000)
새로 추가하는 간선을 경유하는 경로와 그렇지 않은 경로 중에 길이가 $k$ 이하이면서 $k$와 홀짝이 같은 것이 존재하는지 확인한다.
CF 1380E. Merging Towers (2300)
위에 나온 크루스칼의 공 문제와 유사하며 이 문제가 집합의 크기를 관리하지 않아도 돼서 약간 더 간단하다.
- 루트의 부모는 루트로 지정하든 0번 정점같이 없는 정점으로 지정하든 대부분의 문제에서는 큰 상관이 없다. 아무래도 루트의 부모가 없으니까 그냥 0을 저장하면 직관적이긴 한데, 정점 번호가 0부터 시작하고 0번 정점이 루트가 아닌 문제가 나타날 수도 있기 때문에 주의가 필요하다. [본문으로]
'Algorithm > I. Data Structures & Advanced Algorithms' 카테고리의 다른 글
| 169. Square Root Decomposition (0) | 2024.02.01 |
|---|---|
| 168. Merge Sort Tree (0) | 2024.01.10 |
| 166. Euler Tour Technique (0) | 2024.01.01 |
| 165. Sparse Table (0) | 2023.12.23 |
| 163. GCD Segment Tree (2) | 2023.11.29 |



