백트래킹(퇴각 검색, Backtracking)은 문제의 답이 될 수 있는 경우를 단계별로 확인하면서 가능한 답이나 최적해를 구하는 방법이다. 만약 어떤 단계에서 답이 될 수 없다는 것이 확인되었다면 이전 단계로 돌아간다. 이렇게 이전 단계로 돌아가는 것을 가지치기(Pruning)라고 한다.
백트래킹 역시 명확하게 설명하기 쉬운 개념은 아니기 때문에 예제를 보면서 이해하는 것이 도움이 될 것이다.
BOJ 15649. N과 M (1) (Silver III)
기본적인 백트래킹 문제이다. 함수 $f(k)$가 $k$개의 수를 고른 상태에서 호출된다고 하면, 남아 있는 $(n-k)$개의 수 중 하나를 고르고 $f(k+1)$을 호출한다. 만약 $k = m$일 경우 지금까지 고른 $m$개의 수들을 출력하고 이전 단계로 되돌아간다.
굉장히 유명한 문제이다. $n$개의 퀸을 서로 공격할 수 없게 배치하려면 각각의 행과 열에 퀸이 하나씩 배치되어야 하며 각각의 대각선에도 퀸이 최대 하나만 배치될 수 있다. 각각의 행에 퀸을 정확히 하나 배치하게 되므로 첫 번째 행부터 하나씩 퀸을 놓으면서 가능한 경우를 찾는다. $f(k)$이 $1\text{~}(k-1)$번째 행에 퀸을 서로 공격할 수 없게 배치한 상태에서 호출된다고 하면, $k$번째 행에서 이전에 배치한 퀸들을 서로 공격할 수 없는 위치를 찾아서 각각의 위치에 퀸을 놓고 $f(k+1)$을 호출한다. 어떤 경우는 그런 위치가 없을 수도 있는데, 이때는 이전 단계로 돌아간다. 이렇게 해서 $n$번째 행에 퀸을 놓는 데 성공했다면 정답에 $1$을 더한다.
다음은 $n = 4$일 경우 백트래킹 함수의 작동 예시이다.

가장 먼저 $f(0)$이 호출되고 $1$행에서 퀸을 놓을 수 있는 위치를 찾는다. 아직 퀸이 놓이지 않았기 때문에 네 열 모두 퀸을 놓을 수 있다. 먼저 $1$열에 퀸을 놓아 본다.

첫 번째 칸에 퀸을 놓고 $f(1)$을 호출한다. $2$행 $1$열은 $1$행 $1$열에 놓인 퀸 때문에 퀸을 놓을 수 없다.

$2$행 $1$열에 퀸을 놓을 수 없기 때문에 이 칸에 퀸을 놓는 경우는 더이상 생각하지 않고 $2$행 $2$열로 넘어간다. $2$행 $2$열 역시 $1$행 $1$열에 놓인 퀸 때문에 퀸을 놓을 수 없다.

따라서 이 칸에 퀸을 놓는 경우도 더이상 생각하지 않고 $2$행 $3$열로 넘어간다. 이 칸에는 퀸을 놓을 수 있으므로 퀸을 놓아 본다.

$2$행 $3$열에 퀸을 놓고 $f(2)$를 호출한다. $3$행에서 퀸을 놓을 수 있는 자리를 찾으면 없다는 것을 알 수 있다.
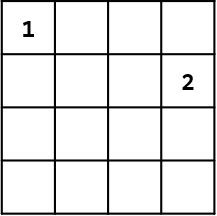
$3$행에서 퀸을 놓을 수 없게 되었으므로 이전 단계로 되돌아간다. $2$행 $4$열로 넘어가면 이 칸에는 퀸을 놓을 수 있다.
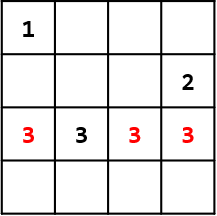
다시 $3$행으로 넘어가면 이번에는 $3$행 $2$열에 퀸을 놓을 수 있다. 이 칸에 퀸을 놓고 $4$행으로 넘어간다.

$4$행에 퀸을 놓을 수 있는 자리가 없으므로 다시 $3$행으로 돌아간다. $3$행에도 퀸을 놓을 수 있는 자리가 더이상 없기 때문에 $2$행으로 돌아가고, $2$행의 모든 칸을 확인했으므로 $1$행으로 돌아간다.

$1$행 $1$열에 퀸을 놓았을 때 $4$개의 퀸을 조건에 맞게 놓을 수 있는 경우가 없었고, $1$행 $2$열로 넘어가 이 칸에 퀸을 놓는다.

$1$행 $2$열에 퀸을 놓을 경우 $2$행에서 퀸을 놓을 수 있는 위치는 $2$행 $4$열이 된다. 이 칸에 퀸을 놓는다.

$3$행으로 넘어가면 $3$행 $1$열에 퀸을 놓을 수 있고, 이 칸에 퀸을 놓고 $4$행으로 넘어가면 $4$행 $3$열에 퀸을 놓을 수 있으므로 $4$개의 퀸을 조건에 맞게 모두 놓았다. 가능한 경우에 $1$을 더하고 이전 단계로 되돌아간다. 탐색을 계속 진행하면 $1$행 $2$열에 퀸을 놓았을 경우 $4$개의 퀸을 조건에 맞게 모두 놓는 방법이 더이상 없음을 알 수 있다.

$1$행의 퀸을 $1$행 $3$열, $1$행 $4$열에 놓고 계속해서 탐색하면 위와 같은 방법을 찾아낼 수 있다. 더이상 가능한 경우가 없으므로 최종 답은 $2$가 된다.
$n$이 $15$일 경우 각각의 행에서 서로 다른 열을 선택하는 경우의 수만 $15!$이지만 가지치기를 하기 때문에 실제로 확인하는 경우는 그것보다 훨씬 적고, 제한시간 내에 문제를 풀 수 있다.
또한 이전에 놓인 퀸들과 서로 공격하게 되는 경우가 있는지를 빠르게 확인할 수 있어야 하는데, 퀸을 놓을 때마다 그 칸이 포함된 열, 대각선에 퀸이 있다는 것을 표시한다. 대각선의 경우 정방향 대각선은 $($행 번호$)-($열 번호$)$가 일정하고 역방향 대각선은 $($행 번호$)+($열 번호$)$가 일정하다는 사실을 이용해서 빠르게 체크할 수 있다.
[연습문제]
한 자리 소수 $2, 3, 5, 7$에서 시작한다. 각각의 수 뒤에 $1, 3, 7, 9$를 붙여나가면서 소수인지 확인하고, 소수가 아니라면 이전 단계로 되돌아간다. 소수일 경우 $1, 3, 7, 9$를 뒤에 붙이는 과정을 수가 $n$자리가 될 때까지 반복한다. 참고로 $n$의 제한이 $8$까지인 이유는 이 조건을 만족하는 $9$자리 이상의 소수가 존재하지 않기 때문이다.
'Algorithm > B. Basic Algorithms' 카테고리의 다른 글
| 25. Divide and Conquer (0) | 2021.02.04 |
|---|---|
| 24. Dynamic Programming & Memoization (0) | 2021.01.31 |
| 22. Recursion (0) | 2021.01.30 |
| 21. Greedy (0) | 2021.01.29 |
| 20. Simulation (0) | 2021.01.29 |



