앞선 글에서 문자열의 표현에 관한 내용들을 다루었고, 이제부터는 문자열의 검색에 대한 내용을 다룬다. 본격적인 내용을 설명하기에 앞서 용어를 정리한다.
- 어떤 문자열의 부분 문자열(Substring)은 문자열의 앞과 뒤에서 각각 $0$개 이상의 문자를 제거한 다음 남는 문자열을 의미한다. 이 글에서는 문자열 $s$의 부분 문자열을 $s[i, j]$로 표기하며, 이는 $s$의 $i$번째 ~ $j$번째 문자로 이루어진 부분 문자열이라는 뜻이다. 문자열의 인덱스는 0-based이다.
- 문자열의 접두사(Prefix)는 문자열의 뒤에서 $0$개 이상의 문자를 제거한 다음 남는 문자열을 의미한다.
- 문자열의 접미사(Suffix)는 문자열의 앞에서 $0$개 이상의 문자를 제거한 다음 남는 문자열을 의미한다.
- 문자열 $s$의 길이를 $|s|$로 나타낸다.
문자열을 검색한다는 것은 어떤 문자열 $s$에 다른 문자열 $t$가 부분 문자열로 존재하는지를, 또한 존재한다면 그 위치는 어디인지를 알아내는 것이다. 문자열 $s$와 $t$의 길이를 각각 $n, m$이라고 하면 $t$가 $s$의 부분 문자열로 존재하는지 확인하는 가장 기본적인 방법은 다음과 같을 것이다.
- $s$의 첫 번째 문자를 $t$의 시작점으로 잡고 $s$와 $t$의 문자를 하나씩 비교한다. 만약 $t$의 모든 문자가 일치한다면 $t$가 부분 문자열로 존재하는 위치를 찾은 것이다.
- $t$의 모든 문자가 일치해서 더이상 남은 문자가 없거나 비교 도중 일치하지 않는 문자가 나왔을 경우 $s$의 다음 문자를 $t$의 시작점으로 잡고 같은 방식으로 다시 비교를 진행한다.
- $s$의 각각의 문자에 대해 위의 과정을 반복한다.
구현은 다음과 같이 할 수 있다. 벡터에는 $t$가 $s$의 부분 문자열로 나타날 때 $t$의 첫 번째 문자열과 대응되는 $s$의 문자의 위치들이 오름차순으로 저장된다.
#import<bits/stdc++.h>
using namespace std;
int main()
{
string s, t;
vector<int>v;
cin >> s >> t;
int n = s.size(), m = t.size(), p;
for(int i = 0; i < n; i++)
{
for(p = 0; p < m && s[i + p] == t[p]; p++);
if(p == m)v.push_back(i);
}
}문자열이 다양한 문자들로 이루어져 있고 별다른 패턴을 갖지 않는다면 코드의 안쪽 for문이 비교적 빠르게 반복을 종료하기 때문에 문자열의 길이가 길어져도 성능이 많이 나빠지지는 않는다. 하지만 이 방법의 기본적인 시간복잡도는 분명 $O(nm)$이다. $s$와 $t$가 다음과 같다고 가정해 보자.
$$s = \ ^\shortparallel \mathsf{a}^\shortparallel \times 10^6$$
$$t = \ ^\shortparallel \mathsf{a}^\shortparallel \times 10^5 + \ ^\shortparallel \mathsf{b}^\shortparallel $$
$s$에는 $a$ 문자밖에 없고, $t$는 $a$ 문자가 계속 이어지다가 마지막에 $b$가 하나 나타난다. 따라서 $s$의 각각의 위치에서 비교를 진행할 경우 $s$가 먼저 끝나는 경우가 아니면 $10$만 개의 $a$가 일치하고 그 다음 글자가 일치하지 않는 상황이 발생한다. 위 예시의 경우 앞쪽 $90$만 개의 위치에서 이런 상황이 발생할 것이고, 나머지 $10$만 개의 위치를 고려하지 않더라도 비교 횟수가 이미 $900$억 번이나 되기 때문에 가능한 모든 경우를 고려해야 하는 PS에서는 이런 방법을 사용할 수 없다.
Knuth-Morris-Pratt Algorithm(KMP)은 위와 같은 경우에도 빠르게 문자열을 검색할 수 있는 알고리즘으로, $\Theta(n+m)$의 시간복잡도로 부분 문자열의 위치를 모두 찾아낸다. KMP의 원리는 문자열을 비교해 나가다가 일치하지 않는 문자가 나왔을 때 이전에 비교한 결과를 바탕으로 다음에 비교할 위치를 빠르게 찾아내는 것이다. 말로만 설명하면 어려우므로 다음과 같은 예시를 생각해 보자.
$$s = \ ^\shortparallel \mathsf{ababcababcabba}^\shortparallel$$
$$t = \ ^\shortparallel \mathsf{abcabb}^\shortparallel$$
다음과 같은 테이블을 만들어 놓고 앞에서부터 한 글자씩 비교를 시작한다. 현재 $s$에서 비교를 시작하는 위치는 $0$이다.

처음에는 두 글자가 일치하고 세 번째 글자에서 일치하지 않는다.

이때 KMP 알고리즘은 시작 위치를 $1$로 바꿔서 다시 비교하는 과정을 수행하지 않는다. 이유는 앞의 두 글자를 비교한 결과에 의해서 시작 위치가 $1$일 경우 부분 문자열이 되지 않는다고 판단하기 때문이다. 시작 위치가 $1$인 경우를 건너뛰고 시작 위치를 $2$로 바꿔서 계속해서 문자열을 비교한다.

이번에는 한 글자만 일치하고 두 번째 글자에서 일치하지 않는다. 시작 위치를 $3$으로 바꾸고 계속 진행한다.

다섯 글자가 일치하고 여섯 번째 글자에서 불일치가 발생했다. 여기서 KMP 알고리즘은 시작 위치를 세 칸 움직여서 $6$으로 바꾼다. 즉, 시작 위치를 움직였을 때 앞쪽에서 불일치가 발생하는 경우를 전부 건너뛰고 진행하는 것이다. 위 상태의 경우 시작 위치가 $3$일 때 다섯 글자가 일치했다. 즉 $s[3, 7] = t[0, 4]$이다. 여기서 시작 위치가 $4$로 바뀌었다고 하자. 이때 $s[4, 7] \ne t[0, 3]$이라면 앞쪽에서 이미 불일치가 한 번 이상 발생했다는 의미이므로 이 경우를 더이상 고려하지 않아도 된다. 만약 $s[4, 7] = t[0, 3]$일 경우 앞에서 $s[3, 7] = t[0, 4]$임을 확인했기 때문에 $t[1, 4] = s[4, 7] = t[0, 3]$이라는 결론을 얻는다. 즉 $t[0, 3] = s[1, 4]$일 때만 시작 위치가 $4$인 경우를 고려하면 된다. 여기서는 그렇지 않기 때문에 시작 위치가 $4$인 경우를 고려하지 않는다. 시작 위치가 $5$인 경우도 시작 위치가 $4$인 경우와 비슷하다. $t[0, 2] \ne t[2, 4]$이라면 시작 위치가 $5$인 경우를 고려할 필요가 없고, 예시에서 $t[0, 2] \ne t[2, 4]$이므로 시작 위치가 $5$인 경우도 고려하지 않는다. 다음으로 시작 위치가 $6$인 경우, $t[0, 1] = t[3, 4]$이므로 KMP 알고리즘은 시작 위치가 $6$일 때 $t$를 찾을 가능성이 있다고 판단한다. 따라서 시작 위치는 $3$에서 $6$으로 바뀌고 계속해서 비교가 진행된다. 앞에서 비교한 결과로 앞쪽 두 개의 글자는 이미 같다는 것을 알고 있는데, 세 번째 글자가 또 일치하지 않는다.

이 경우는 시작 위치가 $0$인 경우와 비슷하다. 시작 위치를 $2$칸 움직여서 $8$로 바꾸고 계속해서 비교한다. 이번에는 여섯 글자가 모두 일치한다.

따라서 시작 위치가 $8$일 때 $t$가 $s$에 나타난다는 것을 알 수 있다. 문자열을 한 번만 찾으면 되는 경우 여기서 바로 반복을 끝낼 수도 있고, 여러 개의 문자열을 찾거나 나타나는 모든 문자열을 찾아야 하는 경우 계속해서 문자열 비교를 진행한다. 시작 위치를 $3$에서 $6$으로 바꾸었던 방식으로 중간에 건너뛸 시작 위치를 확인하는데, 시작 위치가 $9, 10, 11, 12, 13$인 경우 모두 $t$를 찾을 가능성이 없어서 시작 위치가 바로 $14$로 바뀐다.

시작 위치가 $14$일 때는 한 글자가 일치하고, 두 번째 글자를 비교할 때 $s$의 끝에 도달해서 더이상 확인하지 않고 반복을 종료한다.
위의 과정을 요약하면 다음과 같다.
- $s$와 $t$의 처음부터 한 글자씩 비교한다.
- $t$의 끝에 도달했거나 글자가 일치하지 않을 경우 비교하는 $t$의 위치를 바꾼다. $t$의 위치가 바뀌면 $s$의 시작 위치도 바뀐다.
- 계속해서 비교를 진행하면서 $s$의 끝에 도달하면 비교를 끝낸다.
두 번째 단계에서 비교하는 $t$의 위치를 바꾸는 방법은 위에서 설명했는데, 이것도 요약하면 다음과 같다.
- 현재 $t$에서 불일치가 발생한 문자의 위치가 $k$일 때, 문자열 $t[0, k-1]$보다 짧으면서 $t[0, k-1]$의 접두사도 되고 접미사도 되는 가장 긴 문자열의 길이를 $p$라고 하면 비교 위치를 $k$에서 $p$로 바꾼다.
따라서 $t$의 각각의 접미사에 대해 그 문자열 자신이 아니면서 그 문자열의 접두사도 되고 접미사도 되는 가장 긴 문자열의 길이를 구해야 한다. 앞에서 나온 문자열로 예시를 들면 다음과 같다.
| $k$ | $t[0, k]$ | 접미사이면서 접두사인 가장 긴 부분 문자열 | $f(k)$ |
| $0$ | $\mathsf{a}$ | (없음) | $0$ |
| $1$ | $\mathsf{ab}$ | (없음) | $0$ |
| $2$ | $\mathsf{abc}$ | (없음) | $0$ |
| $3$ | $\mathsf{abca}$ | $\mathsf{a}$ | $1$ |
| $4$ | $\mathsf{abcab}$ | $\mathsf{ab}$ | $2$ |
| $5$ | $\mathsf{abcabb}$ | (없음) | $0$ |
위 표에서 마지막에 나온 $f(k)$가 KMP 알고리즘에서 사용하는 실패 함수(Failure Function)가 된다. 이제 각각의 실패 함수의 값을 구하는 방법이 남았으나, 문자열 $t$에서 $t$를 찾는다고 생각하면 앞쪽의 실패 함수의 값들을 그대로 참조해서 뒤쪽의 실패 함수의 값들을 구할 수 있다. 이때는 시작 위치가 $0$인 경우를 제외하고 시작 위치가 $1$인 경우부터 생각한다. 어차피 $f(0) = 0$으로 고정되기 때문에 이것은 문제가 되지 않는다.

한 글자도 일치하지 않기 때문에 $f(1) = 1$이다. 이런 경우는 그냥 다음 위치부터 다시 비교할 수밖에 없는데, 또 한 글자도 일치하지 않는다.

따라서 $f(2) = 0$이고, 다시 다음 위치로 넘어가서 비교하면 이번에는 두 글자가 일치해서 $f(3) = 1, f(4) = 2$가 된다.

현재 $t$에서 비교하는 위치가 $2$일 때 불일치가 발생했으므로 비교하는 위치를 $f(2)$로 바꾼다. 비교하는 위치가 $k$일 때 $f(k)$의 값은 항상 이미 계산되어 있다는 사실에 유의한다.
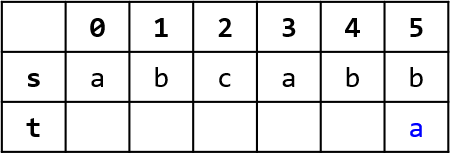
비교하는 위치가 $0$이 되었는데 여전히 일치하지 않으므로 $f(5) = 0$이다. 다음 위치로 넘어가면 $s$의 끝에 도달하게 되고, 모든 실패 함수의 값이 구해졌다. 실패 함수의 값을 구하는 구현은 다음과 같이 할 수 있다.
#import<bits/stdc++.h>
using namespace std;
int f[100005];
int main()
{
string t;
cin >> t;
int m = t.size();
for(int i = 1, j = 0; i < m;)
{
if(t[i] == t[j])
{
f[i] = j + 1;
i++;
j++;
}
else if(j)j = f[j - 1];
else i++;
}
}코드를 짧게 바꾸면 이렇게 쓸 수도 있다. $t$의 길이를 저장하는 변수 $m$이 사라졌고, if문 안의 코드가 한 줄로 줄어들었다.
#import<bits/stdc++.h>
using namespace std;
int f[100005];
int main()
{
string t;
cin >> t;
for(int i = 1, j = 0; t[i];)
{
if(t[i] == t[j])f[i++] = ++j;
else if(j)j = f[j - 1];
else i++;
}
}이 코드는 각각의 실패 함수의 값을 배열에 저장한다. 한 글자도 일치하지 않을 경우를 따로 처리하는 점에 주의한다. 다음으로 문자열 $s$에서 $t$를 찾는 코드를 추가한다.
#import<bits/stdc++.h>
using namespace std;
int f[100005];
int main()
{
string s, t;
vector<int>v;
cin >> s >> t;
int n = s.size(), m = t.size();
for(int i = 1, j = 0; i < m;)
{
if(t[i] == t[j])f[i++] = ++j;
else if(j)j = f[j - 1];
else i++;
}
for(int i = 0, j = 0; i < n;)
{
if(s[i] == t[j])
{
i++;
j++;
if(j == m)v.push_back(i - m);
}
else if(j)j = f[j - 1];
else i++;
}
}이 코드는 처음에 나온 코드와 실행 결과가 같다. 하지만 두 for문 모두 비교 위치를 나타내는 변수 $i$와 $j$가 한 번씩만 초기화되고 각각의 반복에서 두 변수 중 최소한 하나는 값이 증가한다. 따라서 두 번째 반복문을 기준으로 했을 때 $i$는 최대 $n$번 증가할 수 있고 $j$는 최대 $m$번 증가할 수 있으므로 시간복잡도가 $\Theta(n+m)$이 된다.
KMP는 처음 접할 때 이해하기 어려운 알고리즘 중의 하나이지만, 다양한 문자열 문제에 유용하게 쓰일 수 있으므로 잘 이해해 두는 것이 좋다.
[연습문제]
앞에서 나온 코드에 벡터에 저장된 값들을 출력하는 부분만 추가하면 된다. 이 문제는 인덱스가 1-based이므로 저장된 값에 각각 $1$을 더해서 출력해야 한다. KMP 외에도 해싱 등의 다른 방법으로도 풀 수 있다고 한다.
이 문제도 문자열의 마지막 실패 함수의 값을 이용해서 풀 수 있다. 사실 4354번보다 더 간단한데, $L-f(L-1)$이 답이다.
'Algorithm > F. Strings' 카테고리의 다른 글
| 89. Manacher (0) | 2021.08.20 |
|---|---|
| 88. Rabin-Karp (0) | 2021.08.18 |
| 86. Regular Expression (0) | 2021.07.28 |
| 85. Hashing (2) | 2021.07.27 |
| 84. Parsing (0) | 2021.07.24 |



